Tag Archives: Algorithms

What’s Wrong With This Picture?

Battle Lines, Commanders & Computers

When we look at maps of battles even the novice armchair general can quickly trace the battle lines of the armies. Recognizing battle lines is one of the most important skills a commander – or a wargaming Artificial Intelligence (AI) – can possess. Without this ability how will you identify the flanking units? And if you can’t identify the units at the end of a line, how will you implement a flanking attack around them? Equally important is the ability to identify weak points in a battle line.

The algorithm for detecting battle lines and flank units is one of the ‘building block’ algorithms of my TIGER / MATE tactical AI and first appeared in my paper, Implementing the Five Canonical Offensive Maneuvers in a CGI Environment¹⁾http://riverviewai.com/papers/ImplementingManeuvers.pdf. I will discuss how the algorithm works at the end of this blog. For now, just accept that it finds lines and flanks.

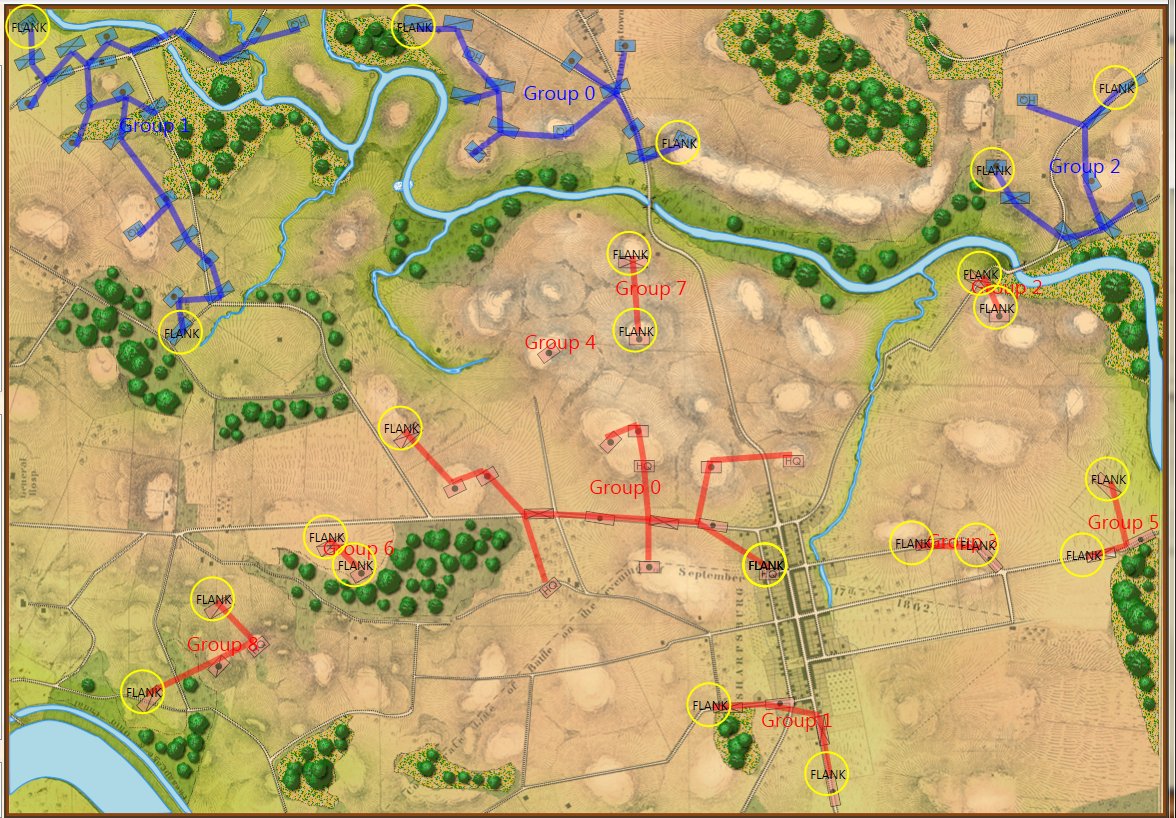
Let’s look at some examples of the General Staff AI ‘parsing’ unit positions. First, the battle of Antietam, situation at dawn (by the way, Antietam is one of the free scenarios included with the General Staff Wargaming System):

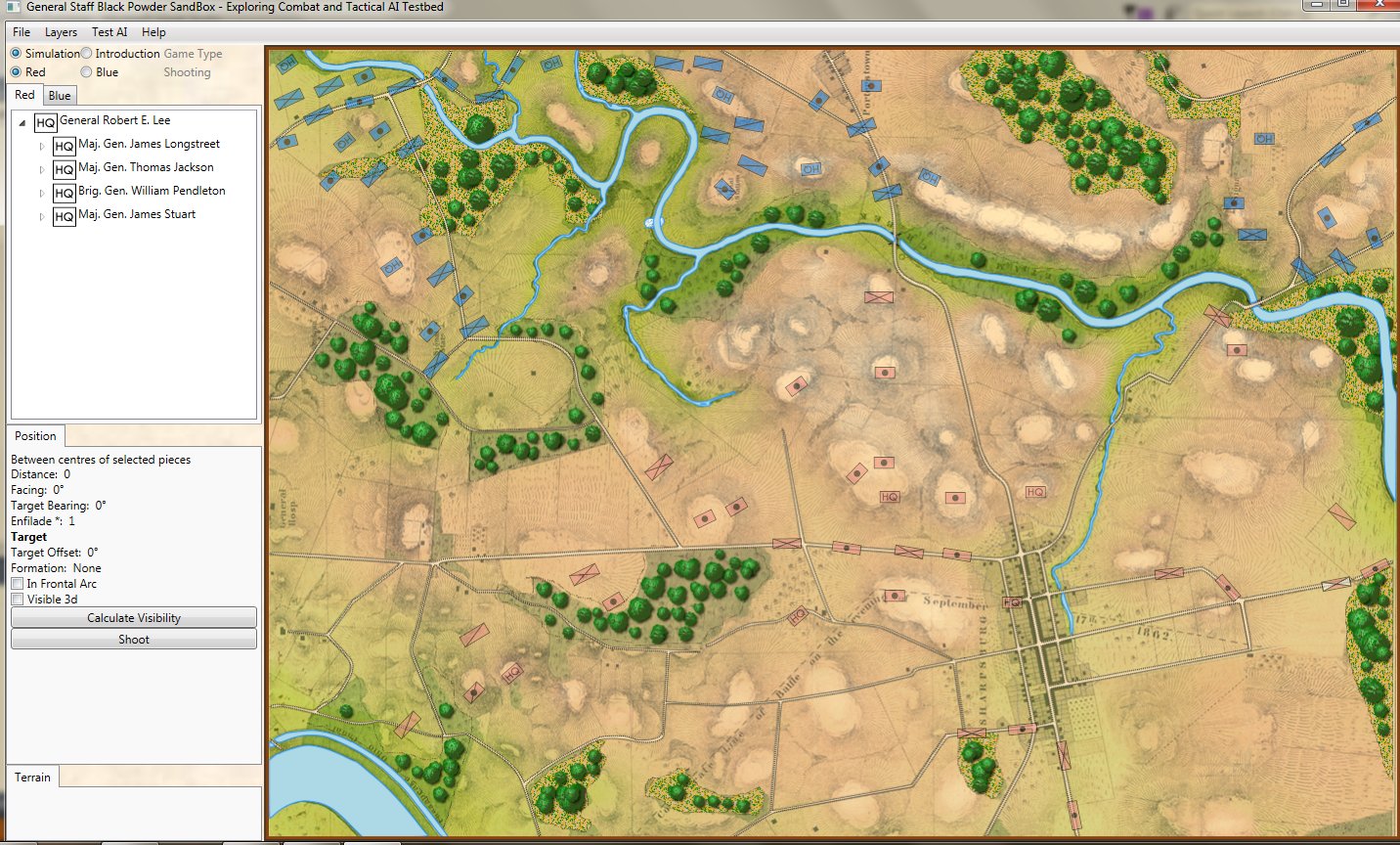
The battle of Antietam, dawn, September 17, 1863. Screen shot from the General Staff Sand Box program. Click to enlarge.

This is how a human sees the tactical situation: units on a topographical map. But, the computer AI sees it quite differently. In the next image, below, the battle lines and elevation are displayed as the AI sees the battle (note: the AI also ‘sees’ the terrain but, for clarity, that is not being shown in this screen capture):

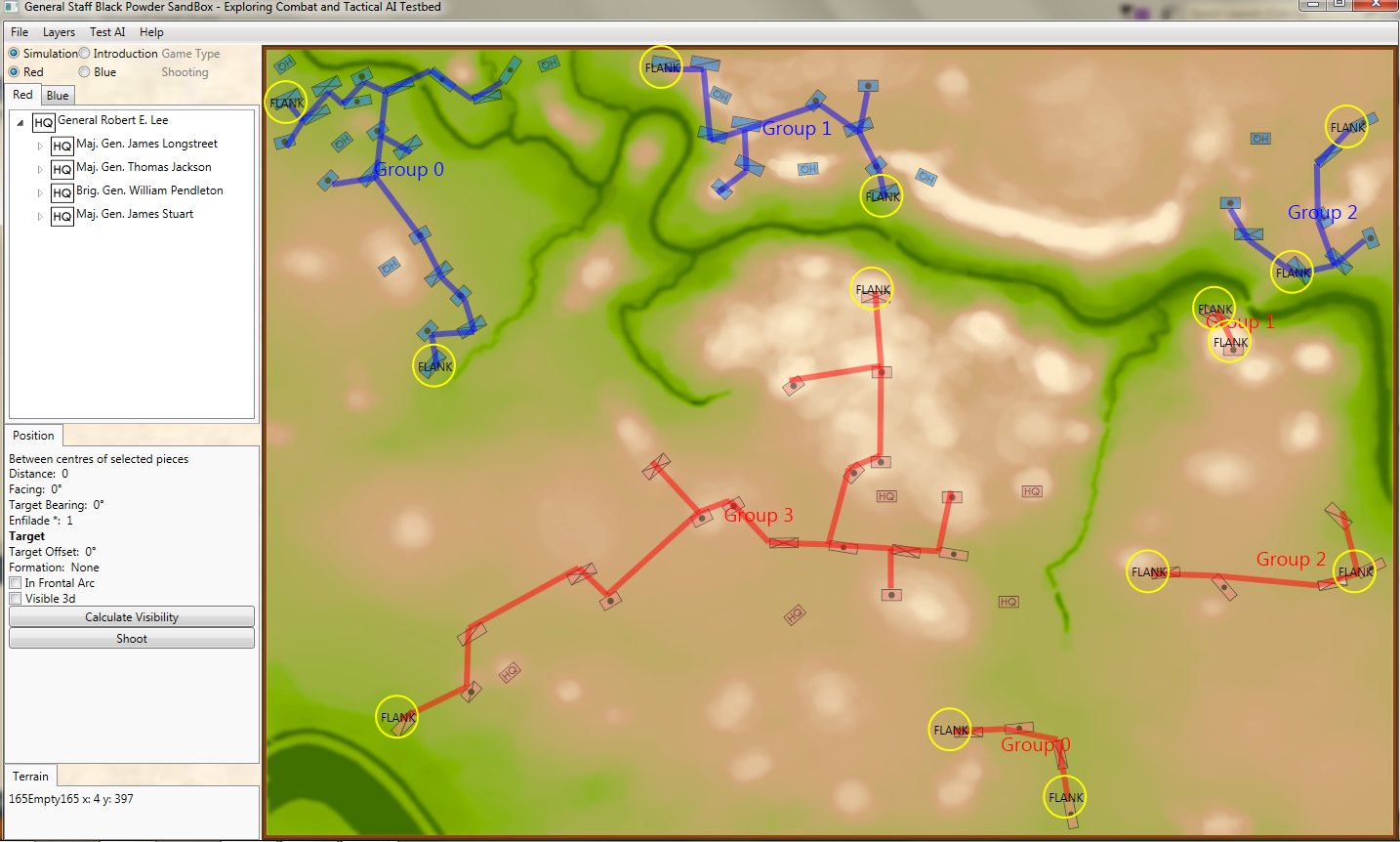
The battle of Antietam, September 17, 1862 dawn, with computer AI battle lines and elevation displayed. Note: the identification of flank units. Both red and blue forces are assembling on the field. Click to enlarge.

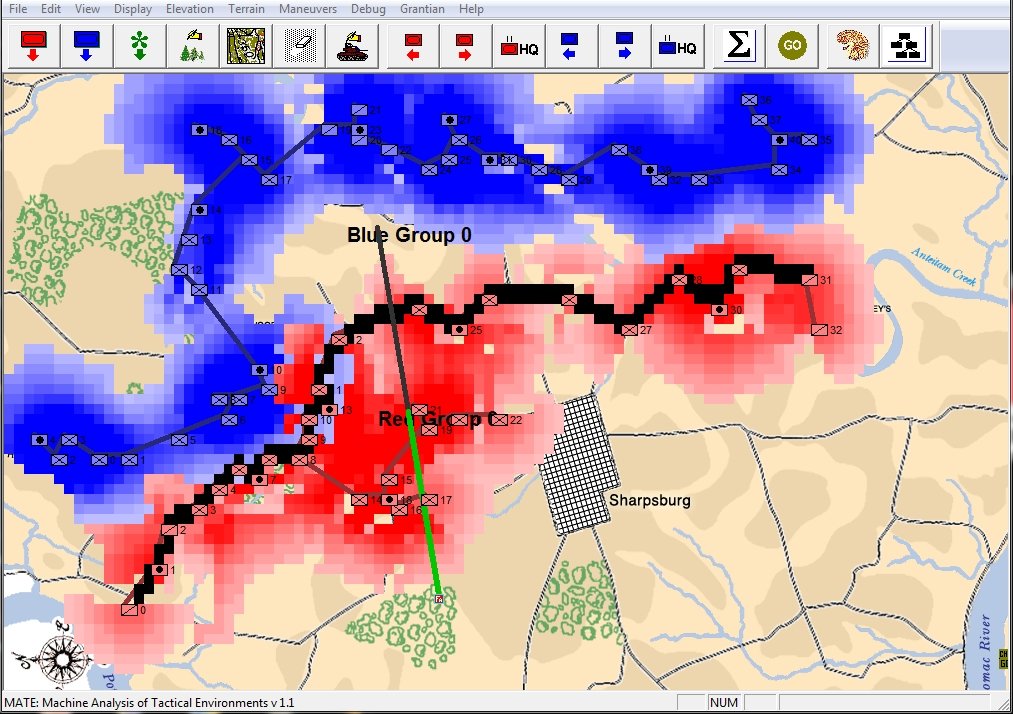
What is immediately obvious is that Red (Confederate) forces are hastily constructing a battle line while Blue (Union) forces are beginning to pour onto the battlefield to attack. Let us now ask the question: what is the weakest point of the Red battle line? Where should Blue attack? This point is sometimes called the Schwerpunkt. German for point of maximum effort²⁾See also, “Clausewitz’s Schwerpunkt Mistranslated from German, Misunderstood in English” Military Review, 2007 https://www.armyupress.army.mil/Portals/7/military-review/Archives/English/MilitaryReview_20070228_art014.pdf. Where should Blue concentrate its forces?

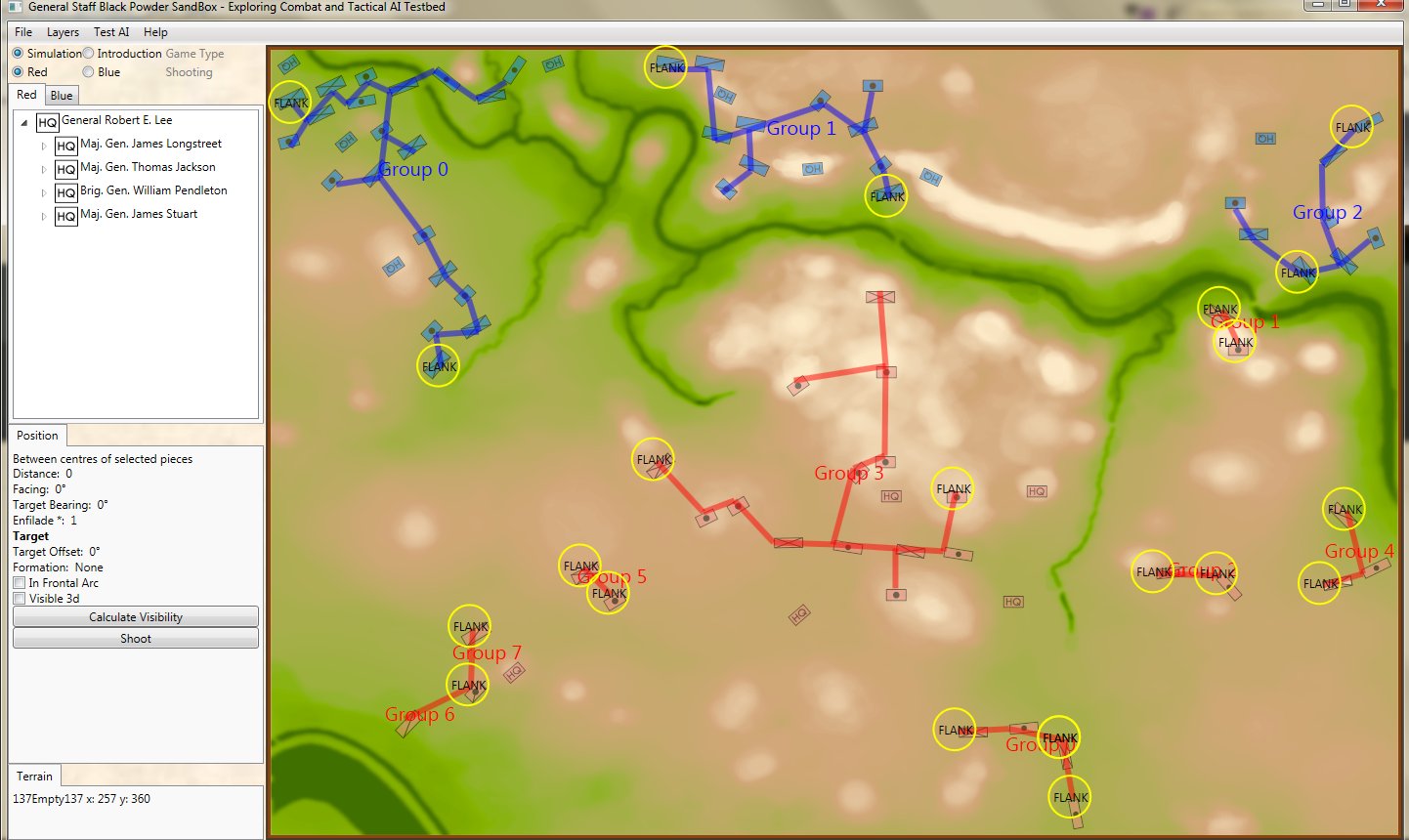
Computer AI representation of battle lines for Antietam, dawn September 17, 1862. The AI is locating the Schwerpunkt or place to attack. Click to enlarge.

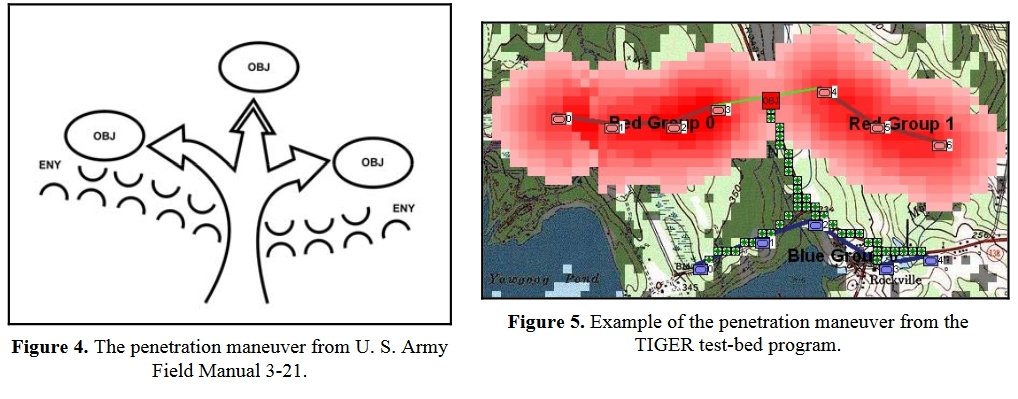
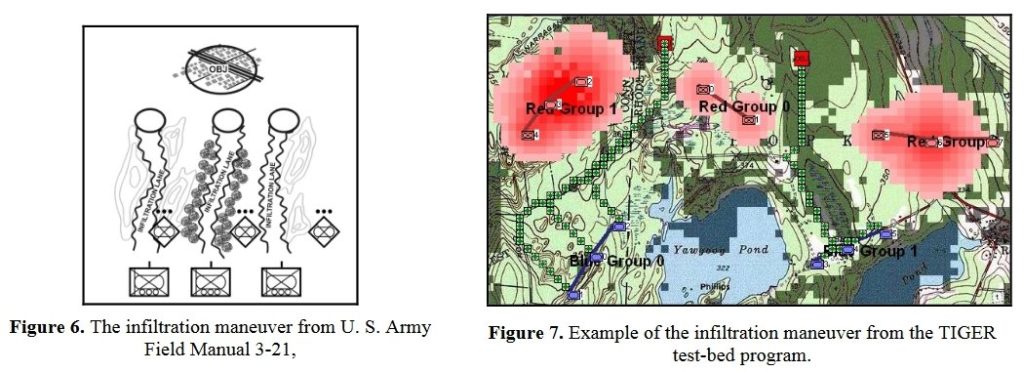
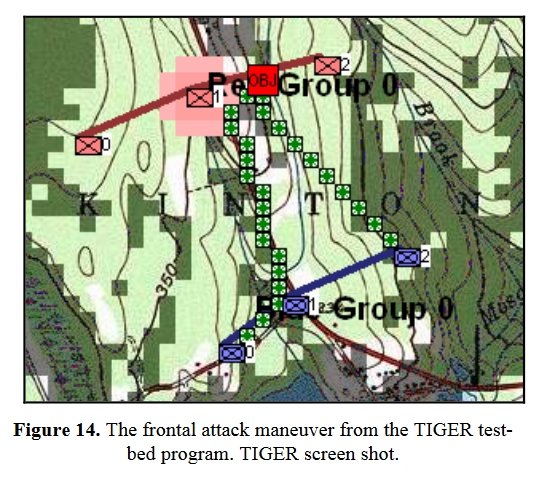
Now that the weakest points of Red’s battle line have been identified, Blue (assuming Blue is being controlled by the AI) can exploit it by attacking the gaps in Red’s battle line. The Blue AI can order either a Penetration or Infiltration Maneuver to exploit these gaps (the following images are from my paper, “Implementing the Five Canonical Offensive Maneuvers in a CGF Environment.” Note, in the TIGER / MATE screen shots below Range of Influence (ROI) is also visible:

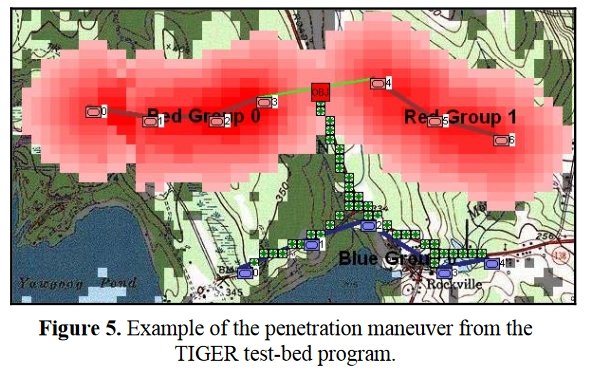
From the paper, “Implementing the Five Canonical Offensive Maneuvers.”

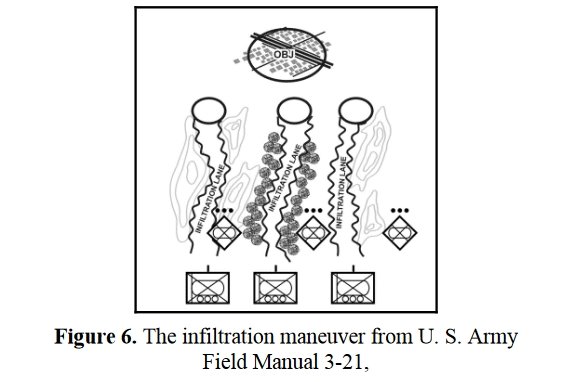
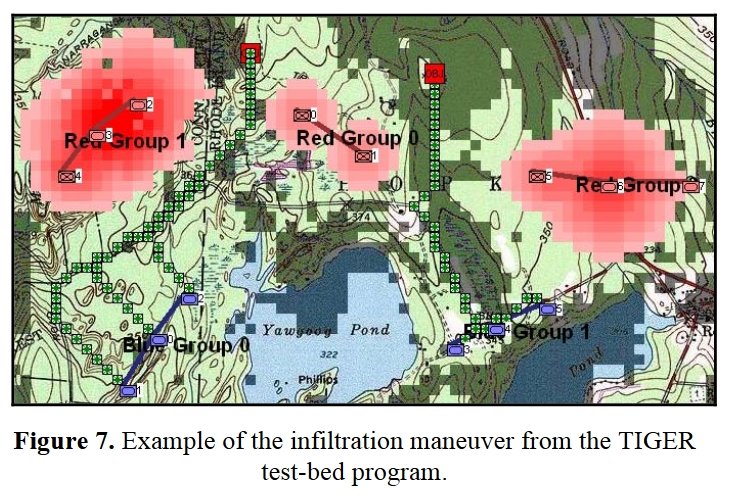Both of these maneuvers are possible because the AI has identified weak points in the OPFOR (Opponent Forces) battle lines. Equally important when discussing battle lines are the location of the flanks. The next two images use the original American Kriegsspiel (1882) map which is also included in the General Staff Wargaming System:

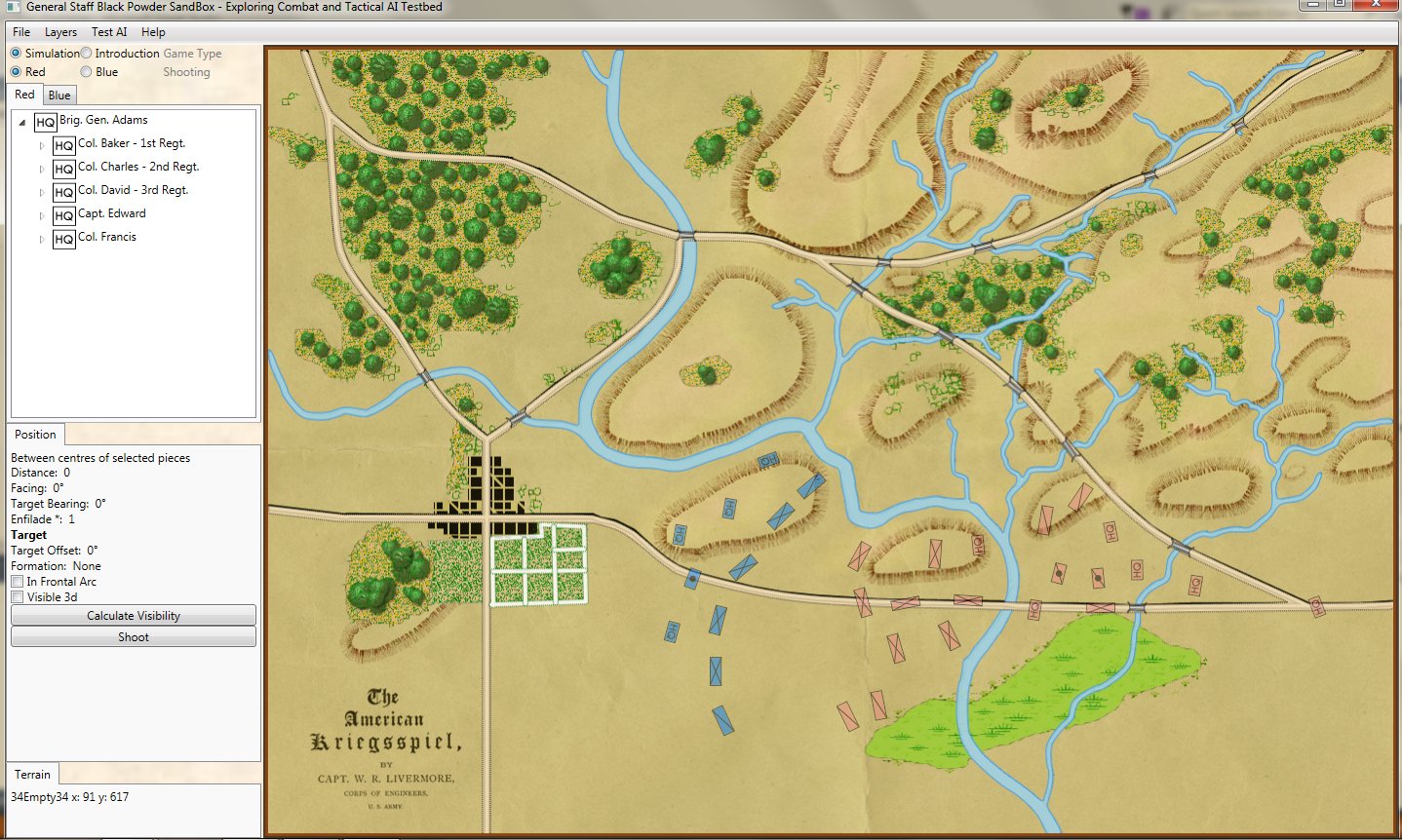
The original American Kriegsspiel map (1882) restored and now used in the General Staff Wargaming System. Screen shot from the General Staff Sand Box AI test program. Click to enlarge.

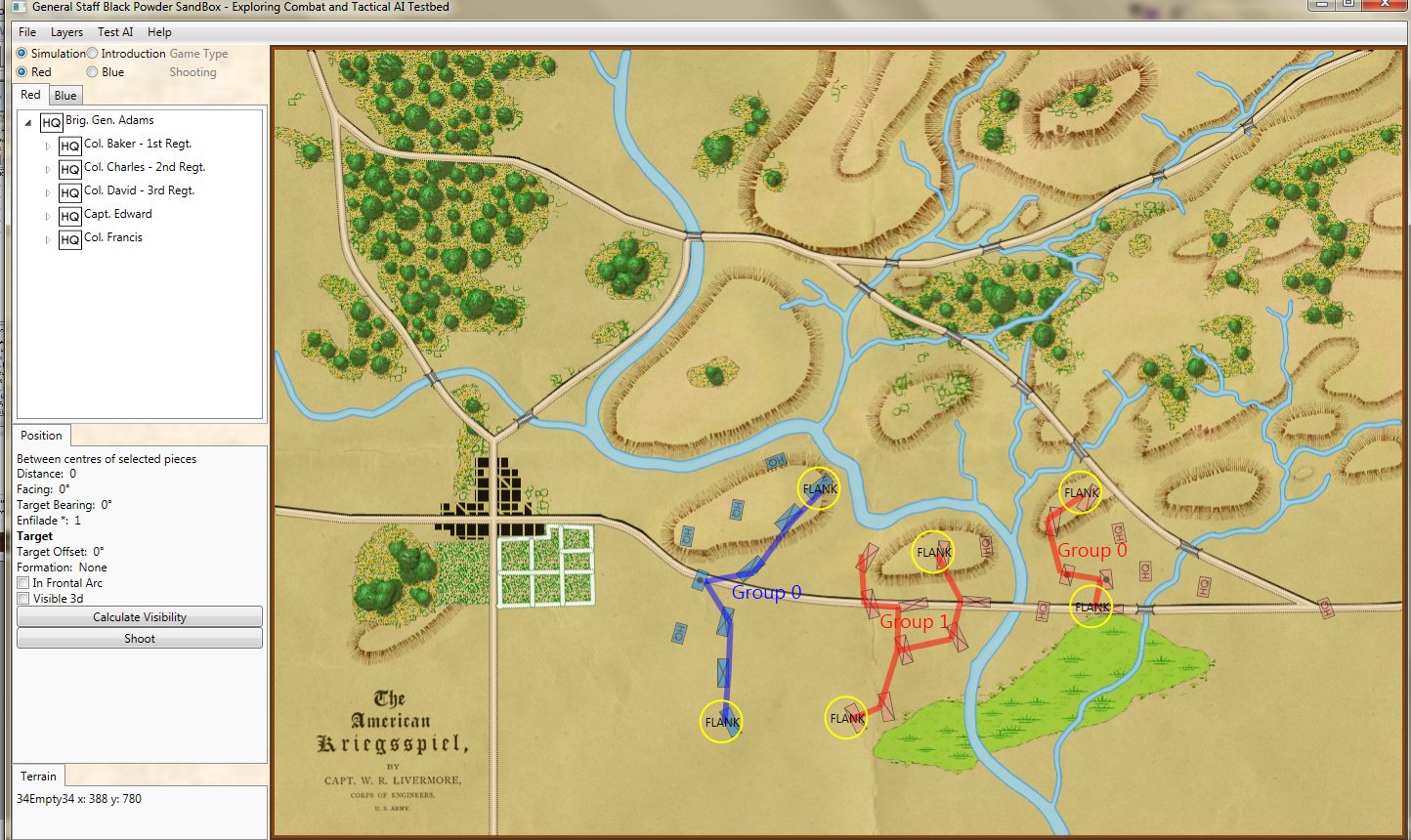
In this screen capture from the General Staff Wargaming System Sand Box AI test program battle lines are displayed by the AI. Note the flank units and especially the unanchored (or open) Blue flank. Click to enlarge.

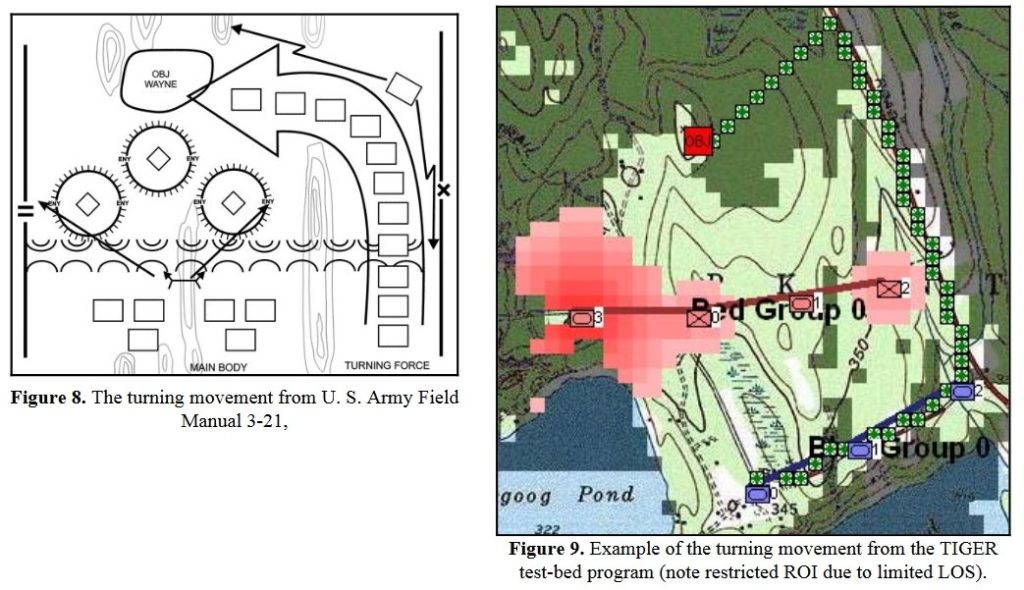
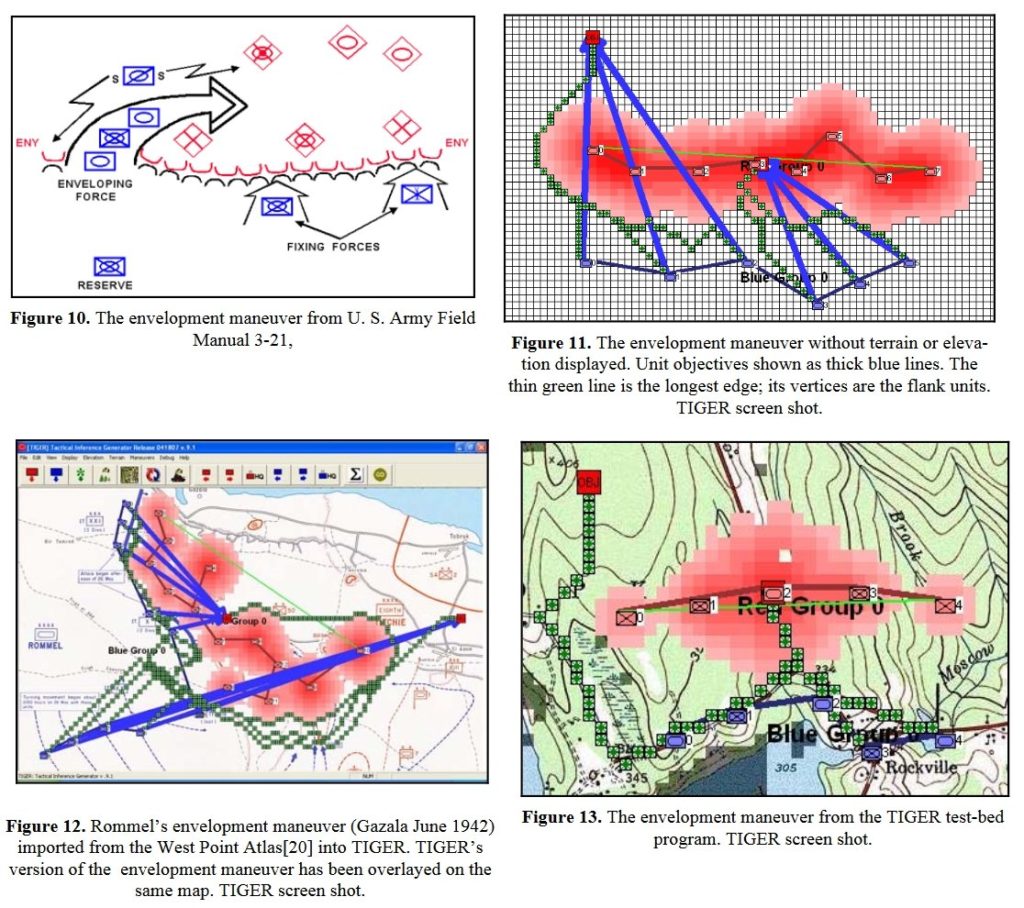
Identifying flank units is vitally important in the Turning Maneuver and the Envelopment Maneuver:

Knowing the location of flank units is also important for classifying tactical positions (this will be the subject of an upcoming blog).

So, how does this algorithm work?

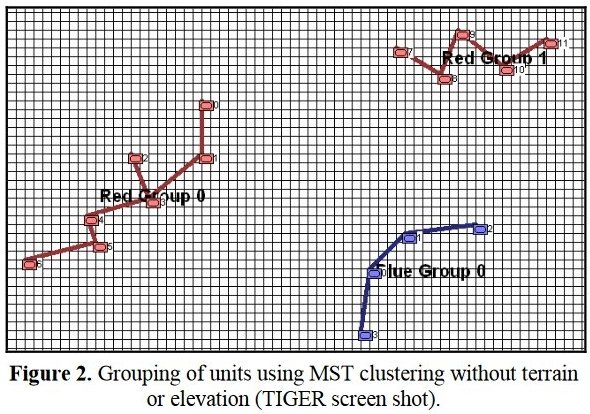
I’ve never been a fan of graph theory; or heavy mathematical lifting in general. One of the required classes in grad school was Design and Analysis of Algorithms and it got into graph theory quite a bit. The whole time I was thinking, “I’m never going to use any of this stuff, but I have to get at least a B+ to graduate,” so I took a lot of notes and studied hard. Later, when I was looking for a framework to understand tactics and to write a tactical AI it became obvious that graph theory was at least part of the solution. Maps are routinely divided into a grid, unit locations can be points (or vertices) at the intersections of these lines. Battle lines can be edges that connect the vertices. I need to publicly thank my doctoral advisor, Dr. Alberto Segre, for first suggesting that battle lines could be described using something called a Minimum Spanning Tree³⁾https://en.wikipedia.org/wiki/Minimum_spanning_tree (MST). An MST is the minimum possible distances (edge weights to be precise) to connect all the vertices in a tree (or a group, as I call them in the above screen shots).

I ended up implementing Kruskal’s algorithm⁴⁾https://en.wikipedia.org/wiki/Kruskal’s_algorithm for identifying battle lines. It is what is called a ‘greedy algorithm’ and it runs in O(E log V) which means it gets slower as we add more units but we’re never dealing with gigantic numbers of individual units in an Order of Battle (probably around 50 is the maximum) so it takes less than a second to calculate and display battle lines for both Red and Blue.

Lastly, and I guess this is my contribution to military graph theory, I realized that the flank units of any battle line must be the maximally separated units. That is to say, that the two units in a battle line that are the farthest apart are the flank units.

Obviously, this is a subject that I find fascinating so please feel free to contact me directly if you have any questions or comments.

References[+]

References
↑1	http://riverviewai.com/papers/ImplementingManeuvers.pdf
↑2	See also, “Clausewitz’s Schwerpunkt Mistranslated from German, Misunderstood in English” Military Review, 2007 https://www.armyupress.army.mil/Portals/7/military-review/Archives/English/MilitaryReview_20070228_art014.pdf
↑3	https://en.wikipedia.org/wiki/Minimum_spanning_tree
↑4	https://en.wikipedia.org/wiki/Kruskal’s_algorithm

A Wargame 55 Years in the Making (Part 3)

4 Replies

The goal of my doctoral research was to create a suite of algorithms that were capable of making ‘human-level’ tactical and strategic decisions. The first step is designing a number of ‘building block’ algorithms, like the least weighted path algorithm that calculates the fastest route between two points on a battlefield while avoiding enemy fire that we saw in last week’s post. Another important building block is Kruskal’s Minimum Spanning Tree algorithm which allows the computer to ‘see’ lines of units.

I use terms like ‘see’ and ‘think’ to describe actions by a computer program. I am not suggesting that current definitions of these terms would accurately apply to computer software. However, it is simply easier to write that a computer ‘sees’ a line of units or ‘thinks’ that this battlefield situation ‘looks’ similar to previously observed battlefields. What is actually happening is that units are represented as nodes (or vertices) in a a graph and some basic geometry is being applied to the problem. Next week we will use probabilities. But, at the end of the day, it’s just math and computers, of course, don’t actually ‘see’ anything.

Examples of how Kruskal’s Minimum Spanning Tree algorithm can be used to separate groups of units into cohesive lines. These figures are taken from, “Implementing the Five Canonical Offensive Maneuvers in a CGF Environment.” by Sidran, D. E. & Segre, A. M.

When you and I look at a map of a battle we immediately see the opposing lines. We see units supporting each other, interior lines of communication, and lines of advance and retreat. The image, below, shows how the program (in this case, TIGER, the Tactical Inference Generator which was written to demonstrate my doctoral research) ‘sees’ the forces at the battle of Antietam. The thick black line is the ‘MST Spine’. You and I automatically perceive this as the ‘front line’ of the Confederate forces, but this is a visual representation of how TIGER calculates the Confederate front line. Also important is that TIGER perceives REDFOR’s flanks as being anchored (that is to say, BLUE does not have a path to the flanking objective, the tip of the green vector, that does not go through RED Range of Influence, ROI, or Zone of Control).

Figure 1. TIGER screen shot of ‘flanking attribute’ calculations for the battle of Antietam (September 17, 1862, 0600 hours). Note the thick black line that repres ents the MST spine of REDFO R Group 0, the extended vectors th at calculate the Flanking Goal Objective Point and BLUEFOR and REDFOR ROI (red and blue shading). REDFOR (Confederate) has anchored flanks.

TIGER screen shot of ‘flanking attribute’ calculations for the battle of Antietam (September 17, 1862, 0600 hours). Note the thick black line that represents the MST spine of REDFOR Group 0, the extended vector that calculates the Flanking Goal Objective Point and BLUEFOR and REDFOR ROI (red and blue shading). REDFOR (Confederate) has anchored flanks. From, “Algorithms for Generating Attribute Values for the Classification of Tactical Situations,” by Sidran, D. E. & Segre, A. M.

Now that TIGER can see the opposing lines and recognize their flanks we can calculate the routes for implementing the Course of Action (COA) for various offensive maneuvers. U. S. Army Field Manual 3-21 indicates that there are five, and only five, offensive maneuvers. The first is the Penetration Maneuver (note: the algorithms for these and the other maneuvers appear in, “Implementing the Five Canonical Offensive Maneuvers in a CGF Environment.” by Sidran, D. E. and Segre, A. M.) and can be downloaded from ResearchGate and Academia.edu.

The Penetration Maneuver is described in U.S. Army Field Manual 3-21 and as implemented by TIGER. Note how TIGER calculates the weakest point of REDFOR’s line. From, “Implementing the Five Canonical Offensive Maneuvers in a CGF Environment.” by Sidran, D. E. and Segre, A. M. Click to enlarge.

The next maneuver is the Infiltration Maneuver. Note that to implement the Infiltration Maneuver, BLUEFOR must be able to infiltrate REDFOR’s lines without entering into RED’s ROI:

The Infiltration Maneuver as described in U.S. Army Field Manual 3-21 and as implemented by TIGER. Note how TIGER reaches the objectives without entering into REDFOR ROI. From, “Implementing the Five Canonical Offensive Maneuvers in a CGF Environment.” by Sidran, D. E. and Segre, A. M. Click to enlarge.

The next maneuver is the Turning Maneuver. Note: in order to ‘turn an enemy’s flanks’ one first must be able to recognize where the flanks of a line are. This is why the earlier building block of the MST Spine is crucial.

The Turning Maneuver as illustrated in U. S. Army Field Manual 3-21 and in TIGER. From, “Implementing the Five Canonical Offensive Maneuvers in a CGF Environment.” by Sidran, D. E. and Segre, A. M. Click to enlarge.

Certainly the most complex offensive maneuver is the Envelopment Maneuver which requires two distinct movements and calculations for the attacking forces: first the attacker must decide which flank (left or right) to go around and then the attacker must designate a portion of his troops as a ‘fixing force’. Think of an envelopment maneuver as similar to the scene in Animal House when Eric “Otter” Stratton (played by Tim Matheson) says to Greg Marmalard (played by James Daughton), “Greg, look at my thumb.” Greg looks at Otter’s left thumb while Otter cold-cocks Marmalard with a roundhouse right. “Gee, you’re dumb,” marvels Otter. In an envelopment maneuver the fixing force is Otter’s left thumb. Its purpose is to hold the attention of the victim while the flanking force (the roundhouse right) sweeps in from ‘out of nowhere’. In the next post I will show a real-world example of an Envelopment Maneuver created by my MATE (Machine Analysis of Tactical Environments) program for DARPA.

The Envelopment Maneuver as shown in U. S. Army Field Manual 3-21 and as implemented in TIGER. From, “Implementing the Five Canonical Offensive Maneuvers in a CGF Environment.” by Sidran, D. E. and Segre, A. M. Click to enlarge.

Lastly, and obviously the maneuver of last resort, is the Frontal Assault:

The Frontal Assault Maneuver from, “Implementing the Five Canonical Offensive Maneuvers in a CGF Environment.” by Sidran, D. E. and Segre, A. M. Click to enlarge.

All that I’ve done in this post is show some of the things that the TIGER program does. What I haven’t done is show how the algorithms work and that’s because they are described in the papers, below. Obviously, this is a subject that I find pretty interesting, so feel free to ask me questions (you can use the Contact Us page).

It is my intention to incorporate these algorithms into the General Staff wargame. However, I’ve been told by a couple of game publishers that users don’t want to play against a human-level AI. What do you think? If you’ve read this far I would really appreciate it if you would answer the survey below.
[os-widget path=”/drezrasidran/survey-11-27″ of=”drezrasidran” comments=”false”]

Papers that were cited in this post with download links:

“An Analysis of Dimdal’s (ex-Jonsson’s) ‘An Optimal Pathfinder for Vehicles in Real-World Terrain Maps'”

In PDF Format

“Algorithms for Generating Attribute Values for the Classification of Tactical Situations.”

In PDF Format

“Implementing the Five Canonical Offensive Maneuvers in a CGF Environment.”

In PDF Format