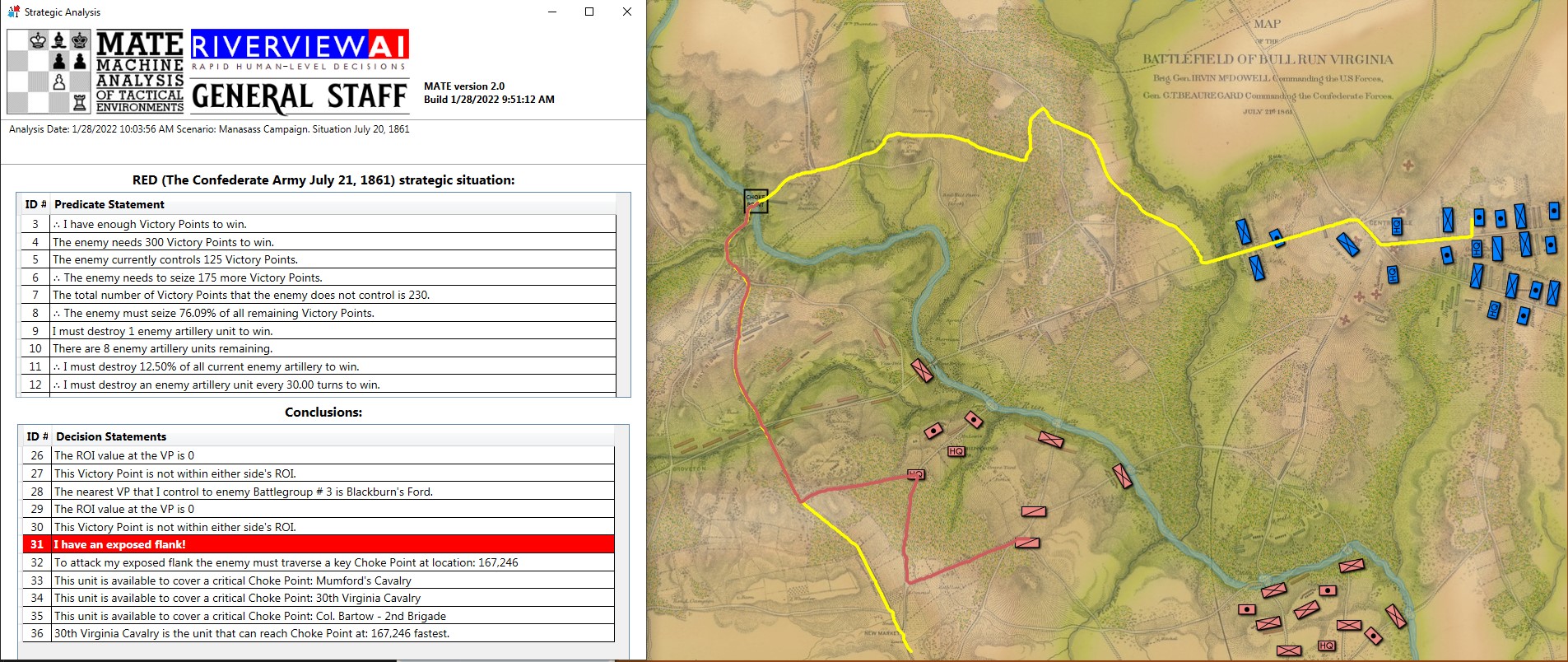
West Point Atlas Map 20; the situation near Manassas & Centreville, July 20, 1861. Click to enlarge. From the Library of Congress; original source.
I‘ve been looking for interesting tactical problems for MATE1)Machine Analysis of Tactical Environments 2.0 to solve and I found a good one after reading William C. Davis’s Battle at Bull Run.2)1995, Stackpole Books, Mechanicsburg, PA The actual battle (called 1st Bull Run by the Union who named battles after nearby waterways and 1st Manassas by the Confederates who labeled battles from nearby geographic features and cities) was a tragicomedy fought on July 21, 1861 in which both commanders (Irvin McDowell for the Union and P. G. T. Beauregard for the Confederates) had little control of their own forces after their initial battle orders were given. Indeed, the battle came down to a series of charges up and down Henry Hill with units committed piecemeal as they arrived on the field. Large elements of both armies were never committed. All in all, not a particularly interesting tactical situation for MATE to analyze.
However, the tactical position the day before (see West Point Atlas map #20, above) is quite a different situation. The Union army is massed at Centreville (Washington, D. C. is off the map, about 30 miles to the east). The two armies are separated by Bull Run which can only be crossed at eleven fords and bridges. Confederate general Beauregard is certain that McDowell’s attack will be almost due south from Centreville and will cross Bull Run at Mitchell’s and Blackburn’s fords. He has assembled almost all of his forces there. This is a tactical situation of which avenues of attack are open and which are closed.
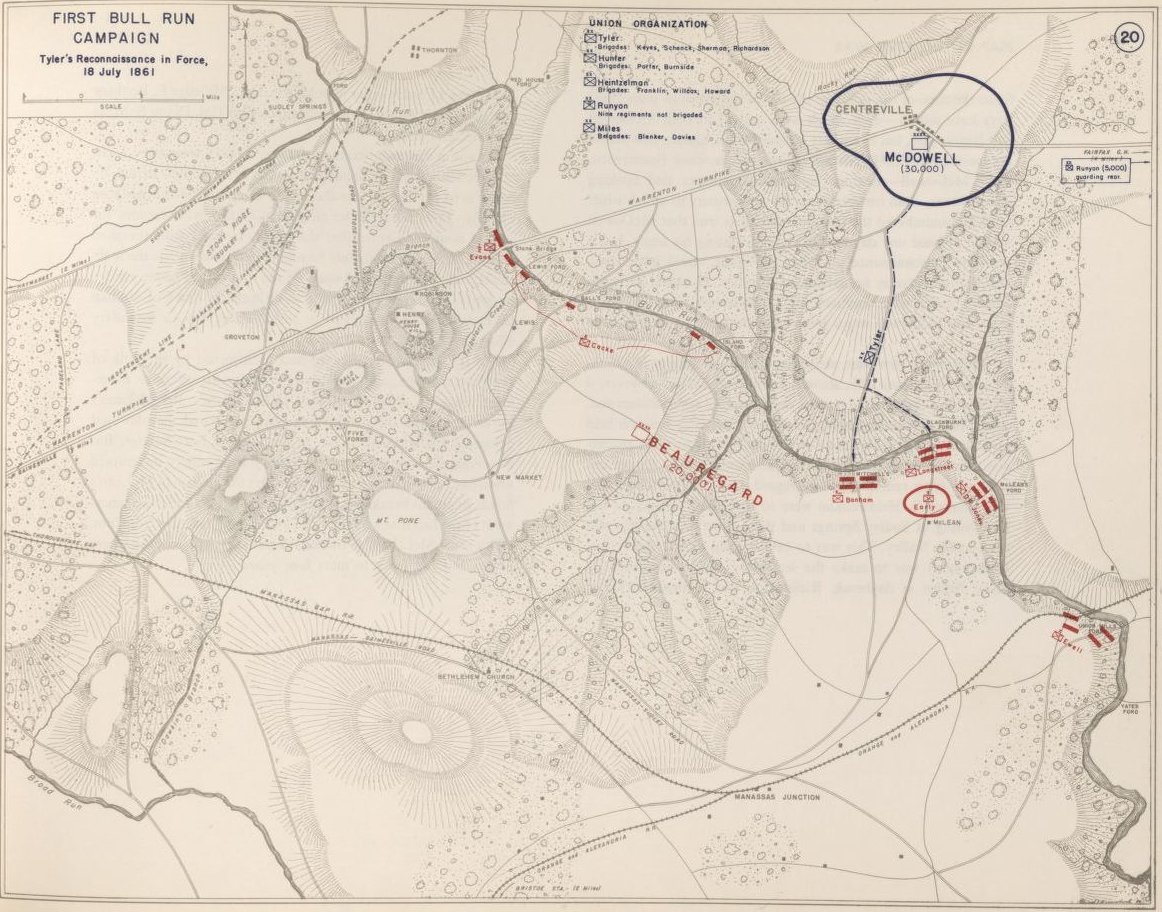
Troop positions and topographical data fed to MATE for this analysis come from the McDowell Map, below:
Map of the battlefield of Bull Run, Virginia. Brig. Gen. Irvin McDowell commanding the U.S. forces, Gen. [P.] G. T. Beauregard commanding the Confederate forces, July 21st 1861 from the Library of Congress. Click to enlarge.
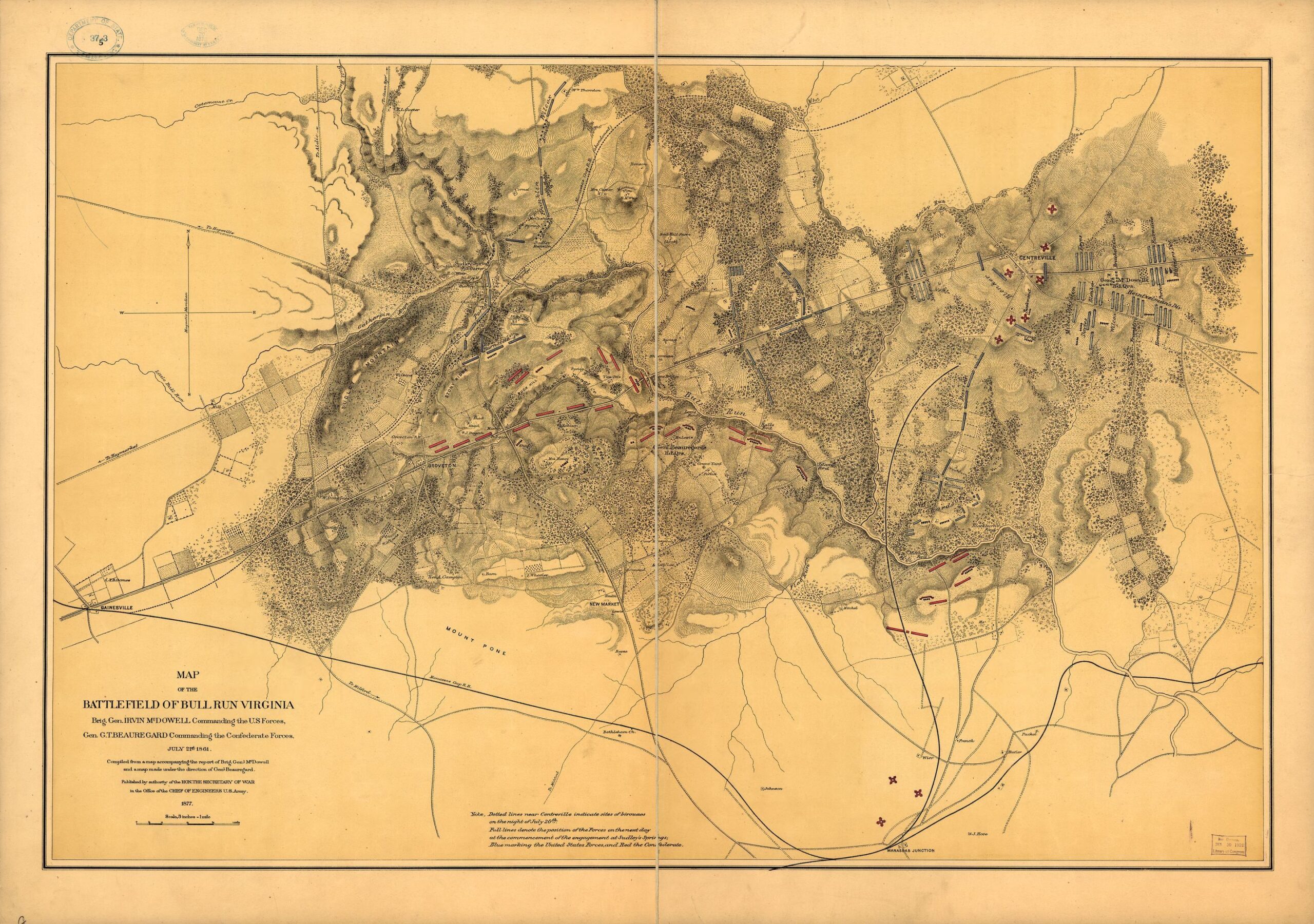
MATE’s assessment of this situation from the Confederate (RED) perspective is below. I use a program called the AI Editor (which, ironically, doesn’t actually edit AI) to observe what MATE is thinking and seeing.
The left window contains a series of predicate statements, conclusions and inferences. Predicate statements to MATE are simple factual statements that MATE knows to be true; e. g. statement #4: The enemy needs 300 Victory Points to win is a basic factual statement. MATE can combine statements (such as #4 and #5: The enemy currently controls 125 Victory Points) to come to a logical conclusion (indicated by beginning the new statement with logical symbol ”∴” or therefore): #6∴ The enemy needs to seize 175 more Victory Points.
The left window is divided into two windows of scrolling text. I printed out the complete list of all statements and conclusions and added commentary (below) so you can follow the thread of MATE’s thought processes:
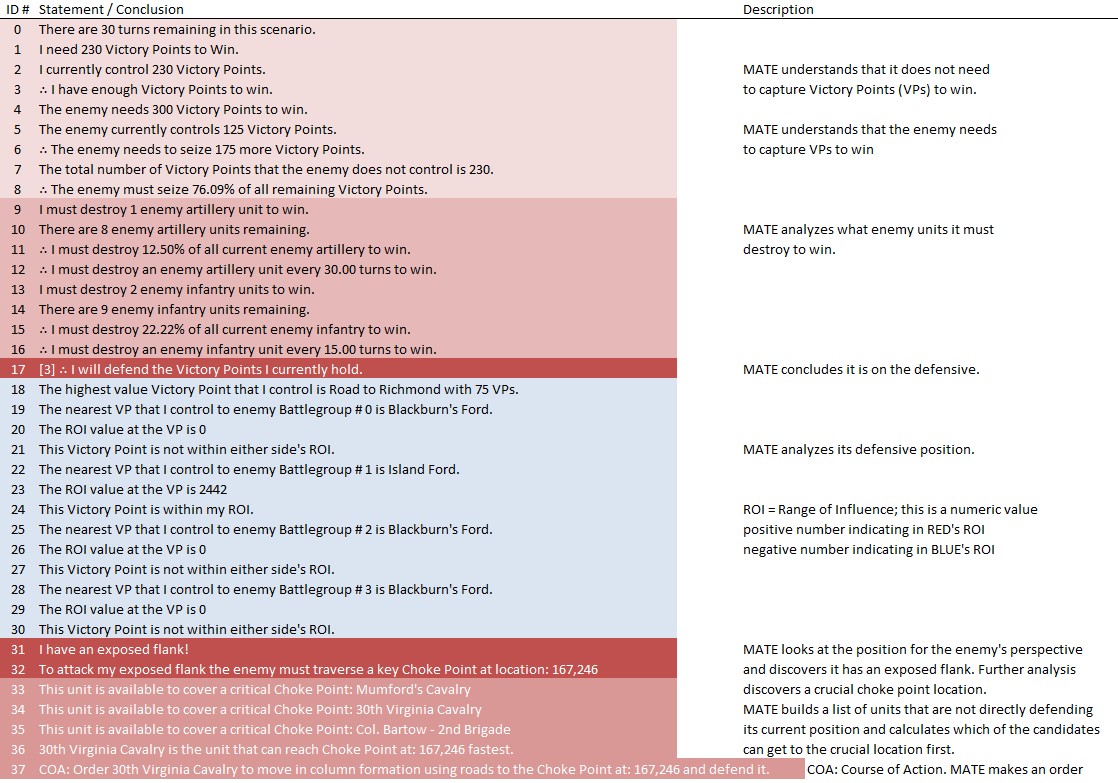
List of premises and conclusions with commentary from MATE’s analysis of Manassas. Click to enlarge.
The right window shows the graphic output of some of MATE’s views of the battlefield (see Layers: Why a Military Simulation Is Like a Parfait). In the above screen shot it is displaying the terrain and elevation layers of the map plus all RED and BLUE forces. The yellow line is how MATE would attack if it were BLUE. Yes, that is correct. MATE analyzes its own defensive position by planning to attack it from the enemy’s perspective. The yellow line (the path using the road net) is how it would turn its own flank. It was this analysis that triggered the creation of statement #31: I have an exposed flank! To see the complete algorithm click here (PDF). The Red line is the optimal route of the 30th Virginia Cavalry to Sudley Ford indicated on the screen by the black box labeled CHOKE POINT.
MATE’s analysis of Manassas certainly appears to be a reasonable analysis and solution to this tactical problem. It also generated a COA (Course of Action) ordering a regiment of cavalry to secure a critical choke point. This, in fact, was better than Confederate General Beauregard’s actual performance.
Is there more work to do? Certainly. MATE uses heuristics. Here is the classic definition of heuristics: “A heuristic function, also simply called a heuristic, is a function that ranks alternatives in search algorithms at each branching step based on available information to decide which branch to follow.”
Here is my definition of a heuristic: a function that groks3)to understand profoundly and intuitively from Heinlein’s Stranger in a Strange Land the problem. MATE uses dozens of heuristic algorithms. MATE is pretty good at discovering – and pouncing – on an exposed flank. MATE groks exposed flanks. MATE also groks interior lines, the high ground, the road net, and constricted avenues of attack and retreat. That may not be a long list but it ticks more boxes than most 19th century generals.
References
| ↑1 | Machine Analysis of Tactical Environments 2.0 |
|---|---|
| ↑2 | 1995, Stackpole Books, Mechanicsburg, PA |
| ↑3 | to understand profoundly and intuitively from Heinlein’s Stranger in a Strange Land |