Tag Archives: A *

Why Machines May Kill Us In Our Sleep

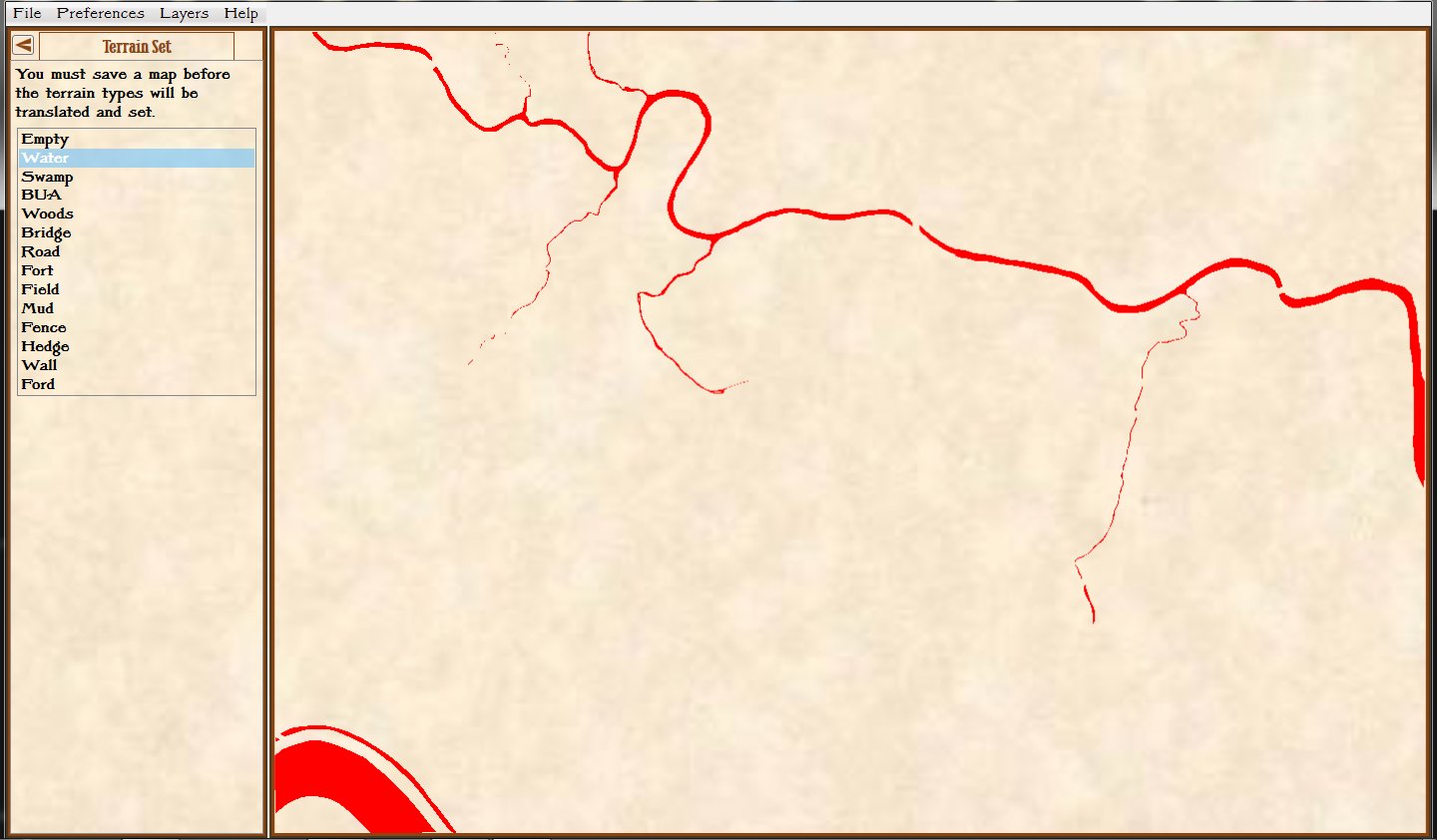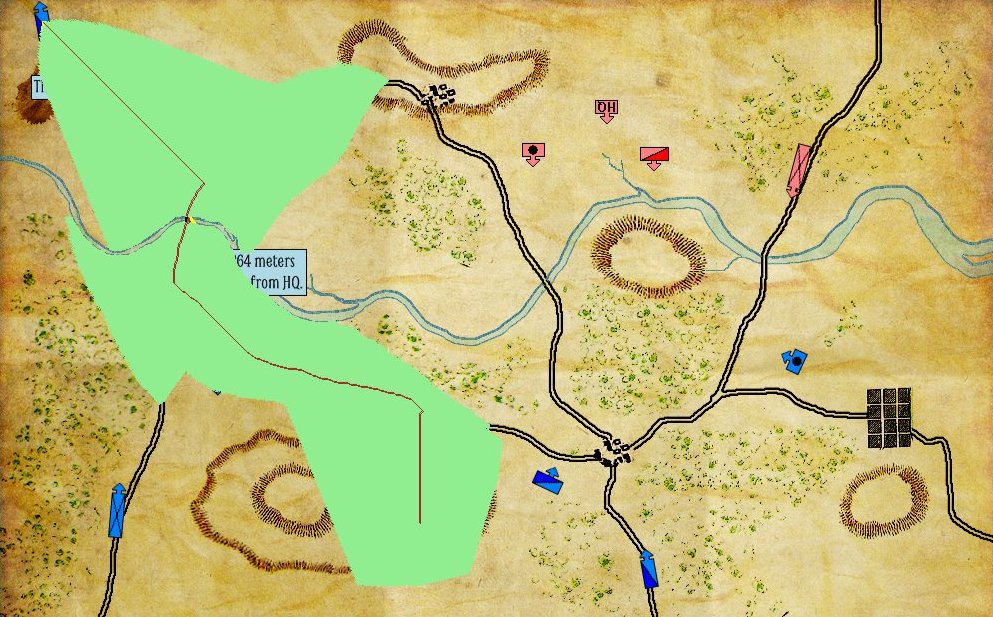
An amazing screen capture of the AI’s solution to a problem. It has found a 1 pixel gap between the data and the edge of the screen and is exploiting it to successfully find an ‘open flank’ of Red. Click to enlarge.

Professor Alberto M. Segre was my thesis advisor and one day he said to me, “You know when your AI is really working because it will surprise you.” Today I got to have one of those weird surprises.

The screen shot (above) is a visual representation of what the AI is up to. You won’t get to see this in the actual game. The program that’s running is called the AI Editor which is a bit of a misnomer because you don’t actually edit the AI in it; you mostly just get to observe what it’s doing. There’s a lot of stuff going on in the above image. There are multiple layers visually displaying different types of data (check out the blog – Layers: Why a Military Simulation is Like a Parfait – for more information about these). But, what interests us are the AI layers: Battle Groups, Objectives, and that thin yellow line that snakes from a group of blue units, crossing Antietam Creek at the Middle Bridge and then, amazingly, exploiting a data anomaly to reach its goal: a point far behind enemy lines.

Some background on the situation:

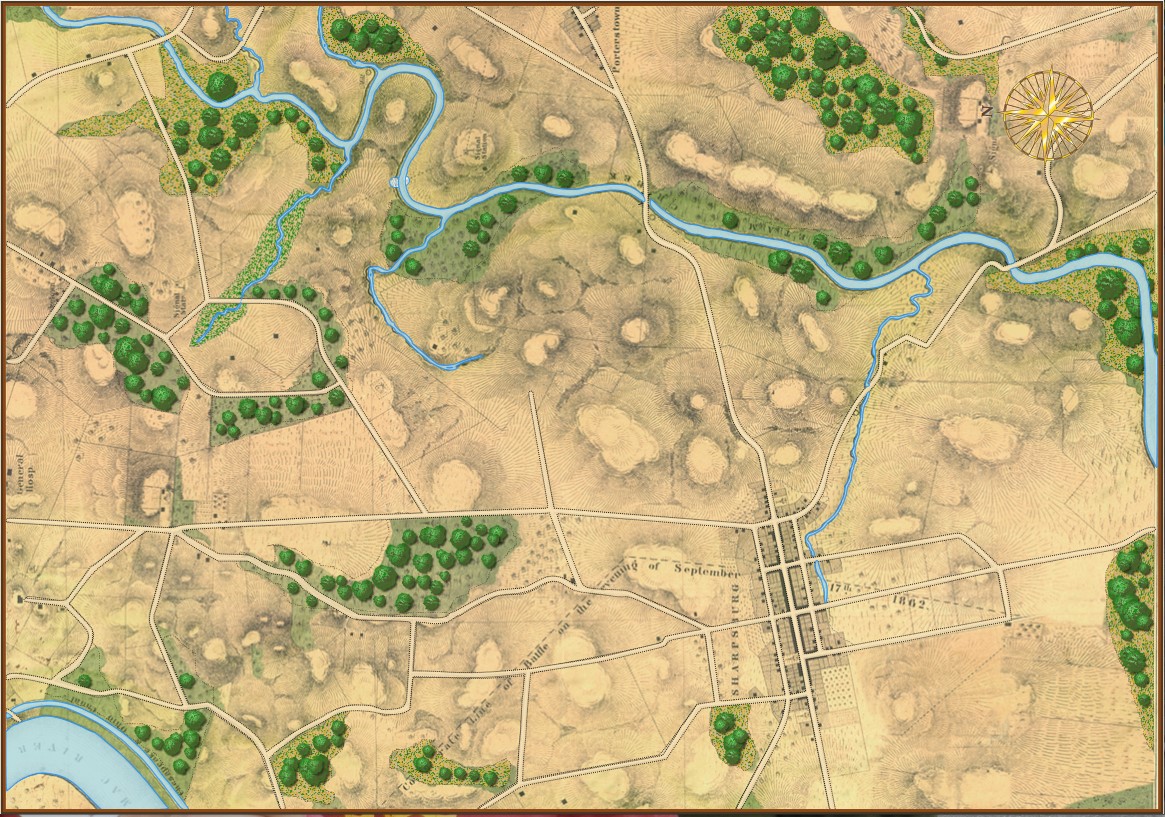
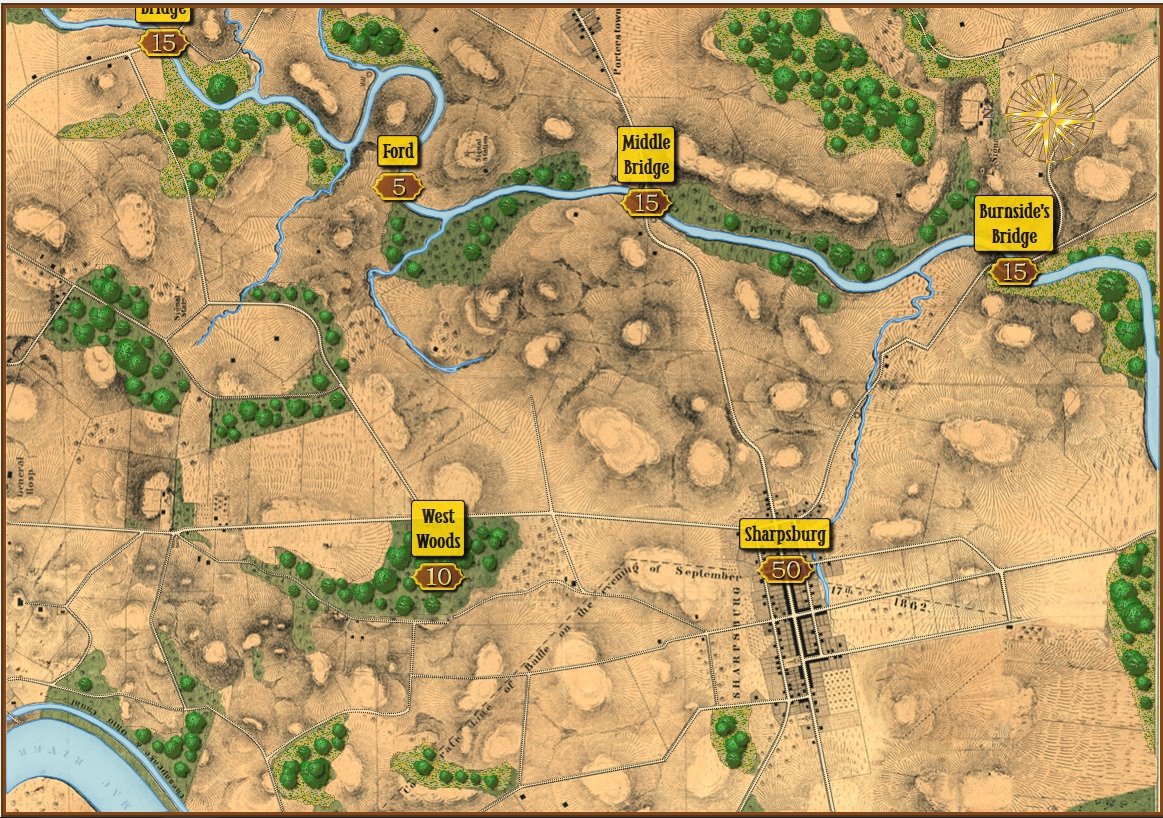
The map of the Antietam Battlefield (screen shot) with terrain and elevation layers displayed. Click to enlarge.

Underlying all the clutter from the first screen capture, top, is the battle of Antietam (above). The map has been rotated 90 degrees to the left so north is now pointing to the left; east is at the top of the screen.

After adding Blue (Union) and Red (Confederate) units to the map in their historical positions at 0600 September 17, 1862 the AI performed a tactical analysis from the perspective of Blue.

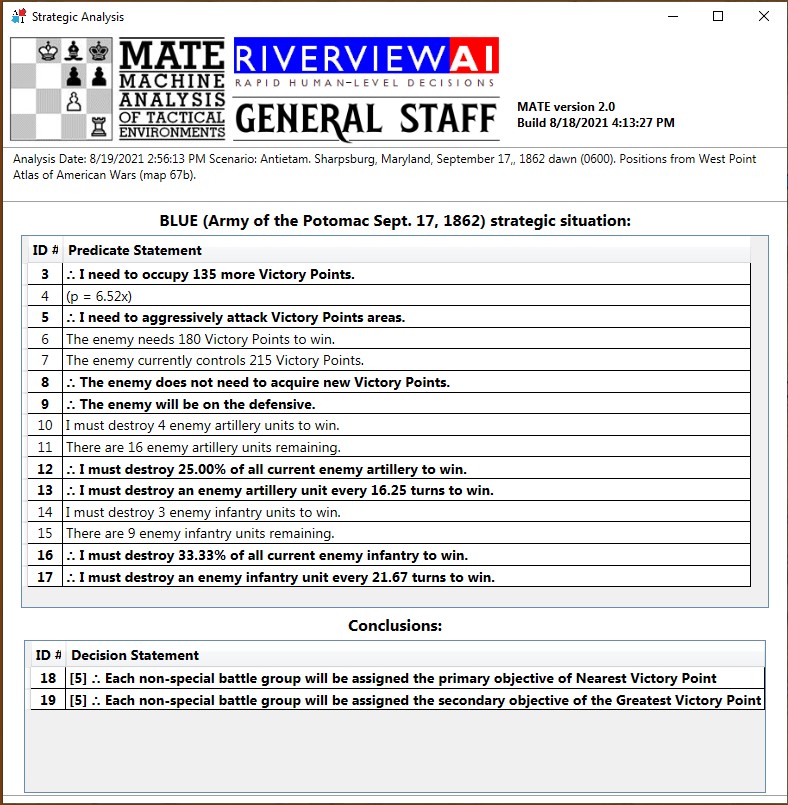
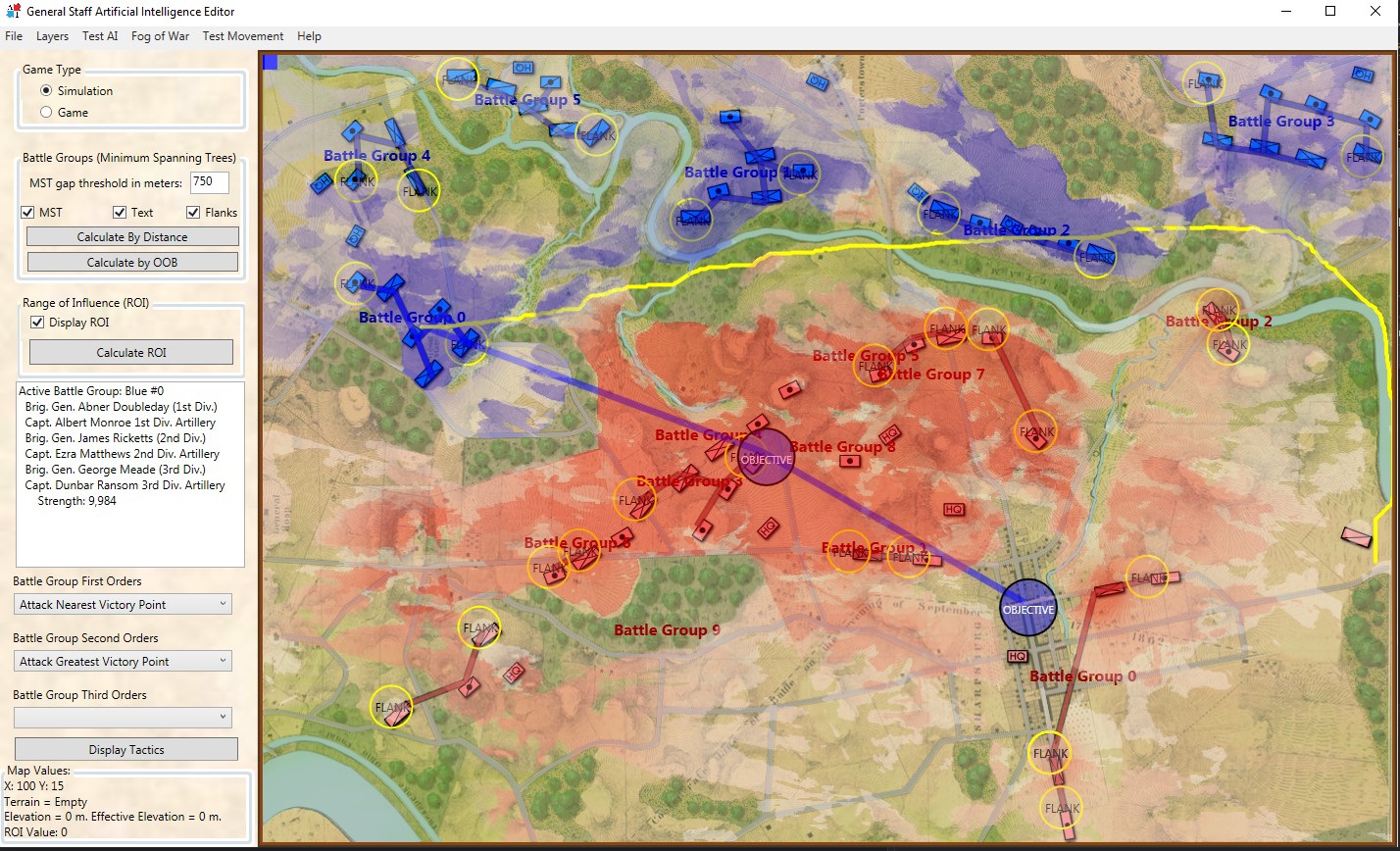
The AI ‘strategic’ analysis for Antietam playing Blue (Union).

The above are a list of Predicate Statements all of which the AI knows to be true. Statements preceded by the logical sign ∴ (therefore) are conclusions, or inferences, derived from the predicate statement referenced in the brackets. It is this analysis that determines if the AI will be on the offensive or defensive and what its objectives will be.

Next, the AI performs Range of Influence (ROI) calculations for the entire observable battlefield. I plan on doing a video about this later, but for now the darker the red (in the topmost screen capture) the more – and more powerful – weapons the Red army can bear on that point. The AI next divides all the units on the map into a forest of minimum spanning trees called Battle Groups. I want to do a video about this, too. However, if you can’t wait, these subjects are covered in my paper, Implementing the Five Canonical Offensive Maneuvers in a CGF Environment (free download).

Again, referring to the top screenshot you can see the AI’s calculations to this point:

It has determined it (Blue) will be on the offensive.
It has calculated enemy ROI.
It has assigned objectives to the first Battle Group.

Flanking Algorithm published in, “Algorithms for Generating Attribute Values for the Classification of Tactical Situations”. Click to enlarge.

Now the AI needs to determine if the enemy has an ‘open or unanchored flank’. In Algorithms for Generating Attribute Values for the Classification of Tactical Situations I published the Algorithm for Flanking Attribute Value Function (right). It basically comes down to this: can the AI trace an unbroken path from the center of the Blue Battle Group to a specific point (called the Retreat Point) far behind enemy lines without crossing into ‘No Go Areas’ (water, swamp) or entering any area controlled by Red’s ROI (literally the red areas in the topmost screen shot).

The reason that I was using Antietam as a test case for anchored / unanchored flanks is because years ago I had analyzed the battle for my doctoral thesis and knew it to be a classic example of anchored flanks; Lee’s left flank rests on the Potomac and his right flank is anchored on the Antietam. Granted, the Confederate flanks were held by Stuart’s cavalry with a little horse artillery support but they were still, by definition, anchored flanks.

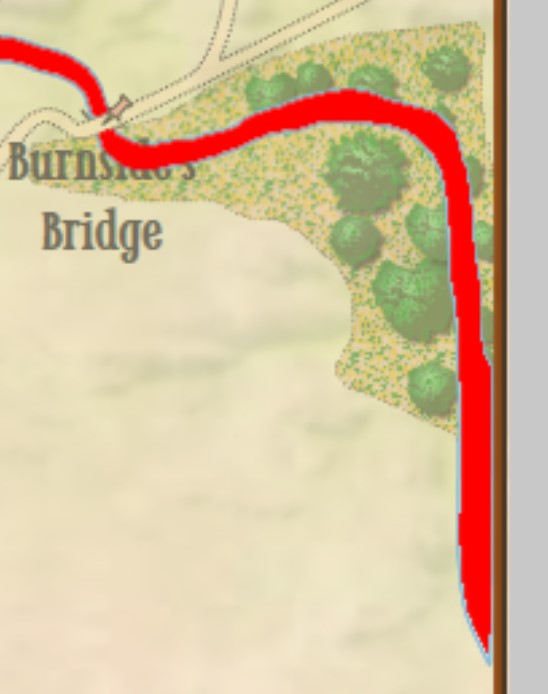Due to an error in the data that made up the Antietam terrain map a 1 pixel (about 3.8 meter wide) strip of ‘no terrain’ was inserted at the far right hand edge of the map (see blow up of screen capture, right; it’s the thin line between the water, represented in red, and the brown edge of the map). This meant there was a ‘land bridge’ across Antietam Creek where none existed in real life. A digital parting of the Red Sea, if you will. But, by the rules of the game the AI perfectly performed its function. There was no error in the AI – again, the AI performed better than I had dared hope – the error was with the data set.

And that’s how fifty years from now I can see a cyber-detective standing over the chalk marks around a body saying, “Yeah, the machine performed perfectly, brilliantly, in fact. But, the error in the data set killed him.”

It’s already happened in real life. For cars with autopilot the data set of the world in which it operates is crucial. However, “against a bright spring sky, the car’s sensors system failed to distinguish a large white 18-wheel truck and trailer crossing the highway, Tesla said. The car attempted to drive full speed under the trailer, “with the bottom of the trailer impacting the windshield of the Model S”, Tesla said.” The driver died. The AI functioned perfectly. But, the error in the data set killed him.

So, I fixed the error in the data set (probably caused by not using the right values in InkScape when I converted the Antietam Water.bmp into paths) and imported it back into the Antietam map using the General Staff Map Editor, saved it out, and ran the AI Editor again and saw this:

The AI did not display a yellow path from the center of the Blue Battle Group to the Red Retreat Point because none existed. Instead, it just wrote the first Predicate Statement in the Tactical Analysis stack: “Red’s flanks are anchored”.

Again, the machine was performing perfectly. And its results were no longer surprising.

Addendum

I recently got to experience this again (though this time it was caused by a different data bug) when I was reviewing the AI’s decisions at the battle of Manassas:

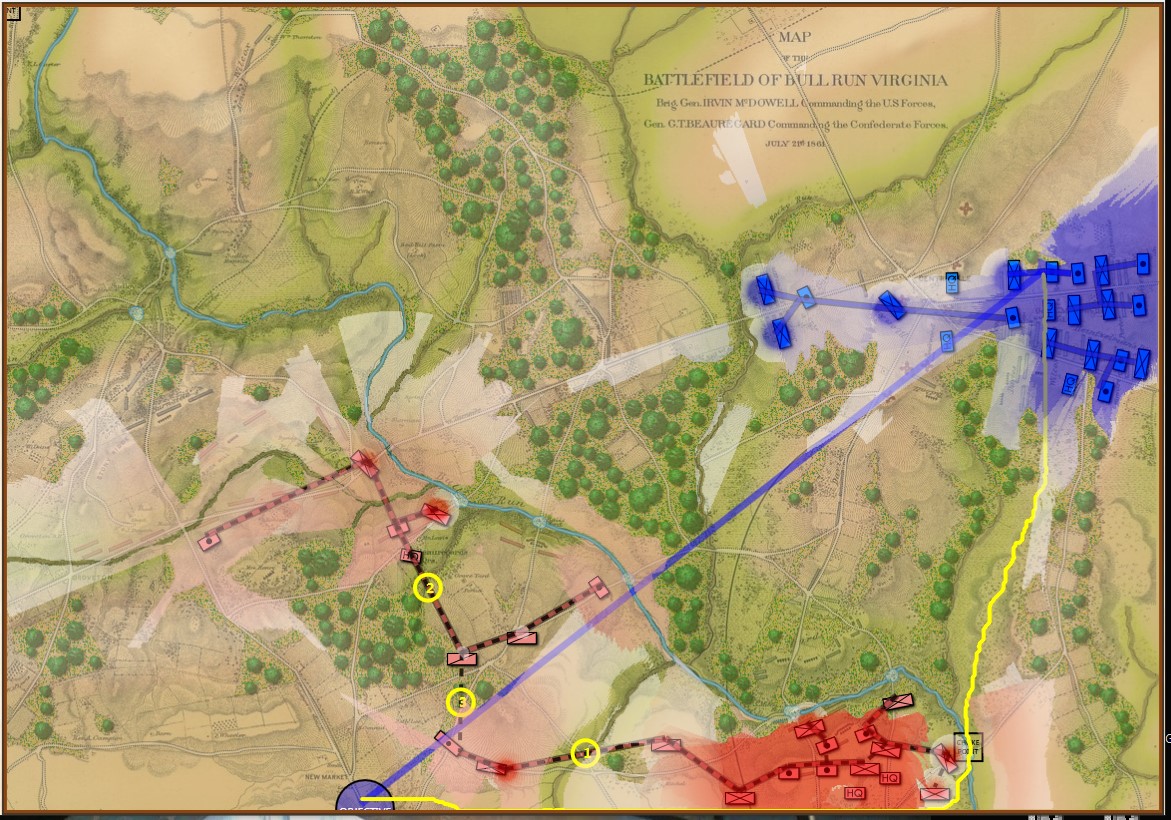
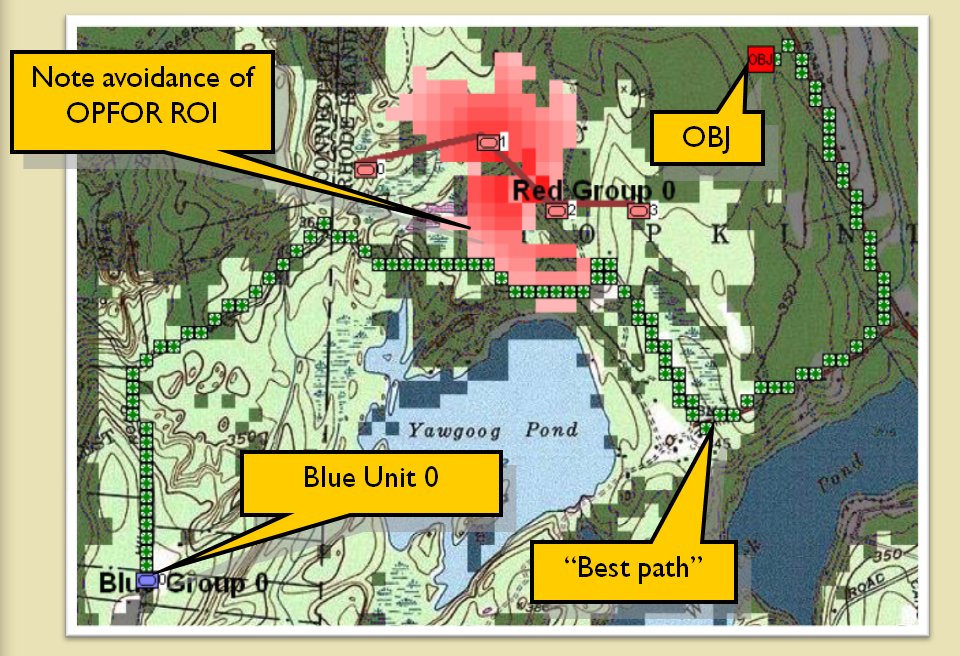
Because the Range of Influence was not calculating the very bottom row the AI found another, perfectly legal, way to reach its goal. Screen shot from the General Staff AI Editor. Click to enlarge.

In this instance, the error in the database was caused by the Range of Influence (basically a map of what red and blue can see and hit) not calculating the very last row. Consequently, the AI was able to legally trace a path from the blue forces in the northeast to their goal at the bottom of the map.

After this bug was corrected the AI performed as expected:

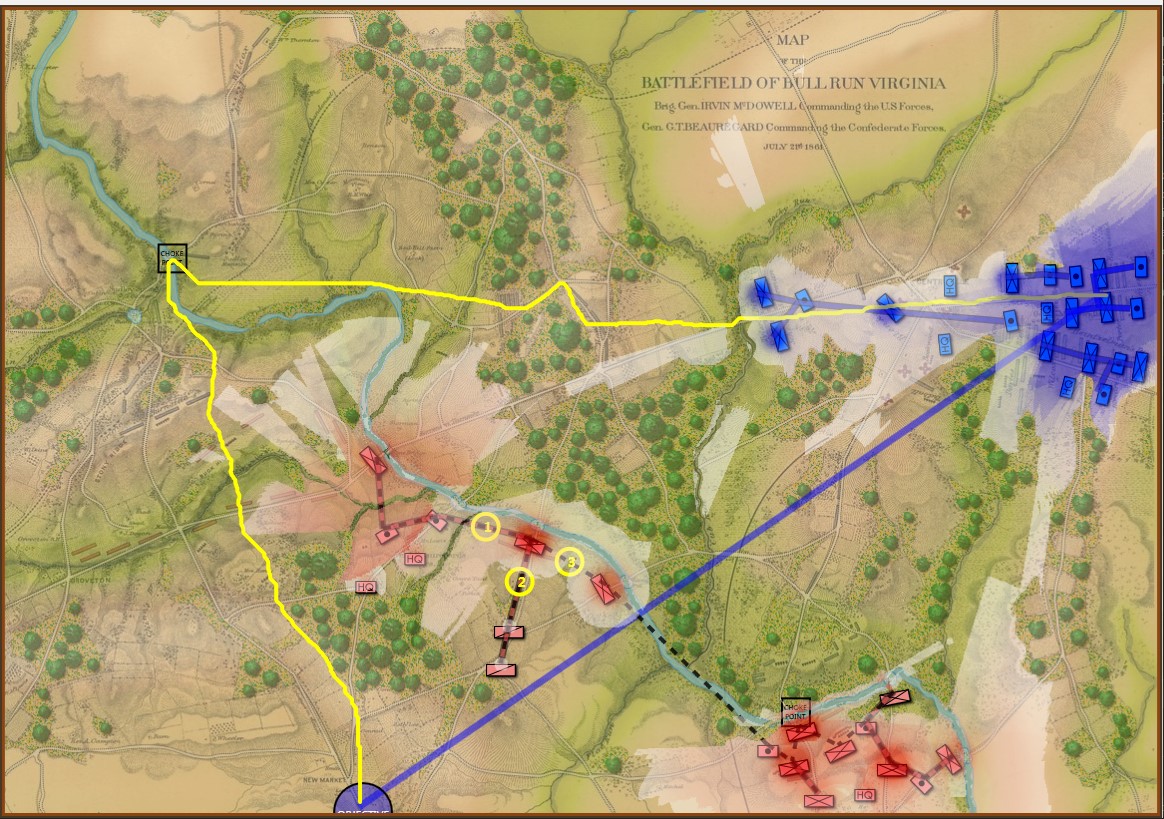
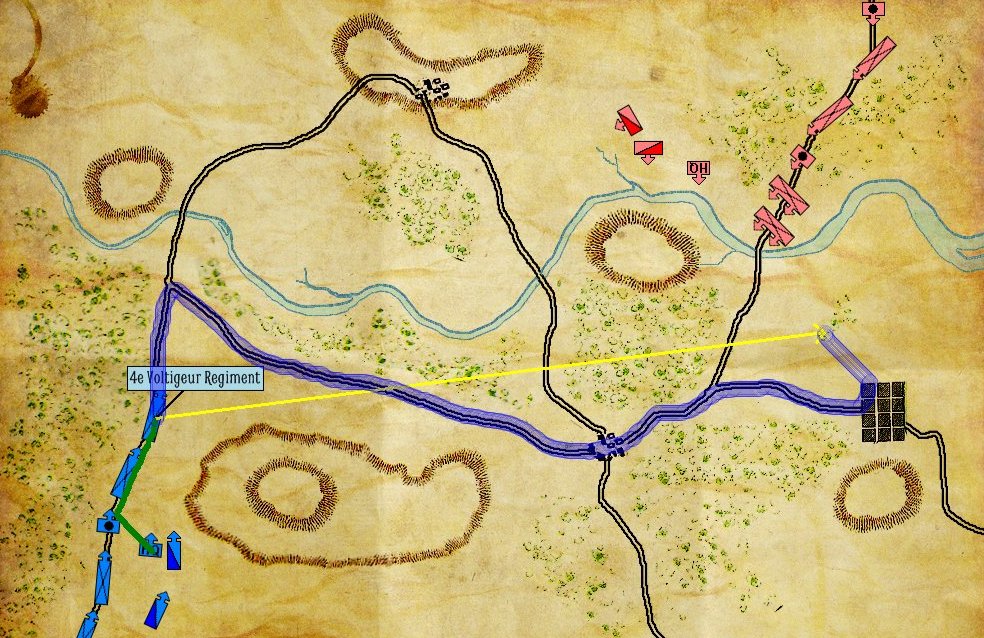
The AI correctly sees going around red’s left flank as the solution to the problem. Screen shot from General Staff AI Engine. Click to enlarge

In the above screen shot the AI has demonstrated the correct solution to the tactical problem facing blue at Manassas on July 20, 1861 (the day before the actual battle). Red’s left flank is unanchored. It’s wide open. Note how the AI identifies the one choke point (Sudley Springs Ford) in the plan.

So, the AI surprised me again. I think it’s looking pretty good. When you play against it, watch your flanks.

Maps, Commanders & Computers

3 Replies

How a map of the battle of Antietam looks to us humans. Screen shot from the General Staff Map Editor. Click to enlarge.

How the computer sees the same map (terrain and elevation). This is actually a screen shot from the Map Editor with the ‘terrain’ and ‘elevation’ layers turned on. Click to enlarge.

Computer vision is the term that we use to describe the process by which a computer ‘sees'¹⁾When describing various AI processes I often use words like ‘see,’ ‘understand,’ and ‘know’ but this should not be taken literally. The last thing I want to do is to get in to a philosophic discussion on computers being sentient. the world in which it operates. Many companies are spending vast sums of money developing driverless or self-driving cars. However, these AI controlled cars have had a number of accidents including four that have resulted in human fatalities.²⁾https://en.wikipedia.org/wiki/List_of_self-driving_car_fatalities The problem with these systems is not in the AI – anybody who has played a game with simulated traffic (LA Noir, Grand Theft Auto, etc.) knows that. Instead, the problem is with the ‘computer vision’; the system that describes the ‘world view’ in which the AI operates. In one fatality, for example, the computer vision failed to distinguish a white semi tractor trailer from the sky.³⁾https://www.theguardian.com/technology/2016/jun/30/tesla-autopilot-death-self-driving-car-elon-musk Consequently, the AI did not ‘know’ there was a semi directly in front of it.

In my doctoral research I created a system by which a program could ‘read’ and ‘understand’ a battlefield map⁴⁾TIGER: An Unsupervised Machine Learning Tactical Inference Generator http://www.riverviewai.com/download/SidranThesis.html. This is the system that we use in General Staff.

The two images, above, show the difference in how a human commander and a computer ‘see’ the same battlefield. In the top image the woods, the hills and the roads are all obvious to us humans.

The bottom, or ‘computer vision’ image, is a bit of a cheat because this is how the computer information is visually displayed to the human designer in the General Staff Map Editor. The bottom image is created from four map layers (any of which can be displayed or turned off):

The four layers that make up a General Staff map.

The background image layer in a General Staff map is the beautiful artwork shown in the top image. The place names and Victory Points layer are also displayed in the top image. The terrain and elevation layers are described below:

The next three images are actual visual representations of the contents of memory where these terrain values are stored (this is built in to the General Staff Map Editor as a debugging tool):

Screen shot from the Map Editor showing just terrain labeled as ‘water’. Click to enlarge

Screen shot from the General Staff Map Editor showing the terrain labeled as ‘woods’. Click to enlarge.

Screen shot from the General Staff Map Editor showing the terrain labeled ‘road’. Click to enlarge.

A heightmap for Antietam. This is a visual representation of elevation in meters (darker = lower, lighter = higher). Click to enlarge.

To computers, an image is a two-dimensional array; like a giant tic-tac-toe or chess board. Every square (or cell) in that board contains a value called the RGB (Red, Green, Blue⁵⁾Except in France where it’s RVB for Rouge, Vert, Bleu ) value. Colors are described by their RGB value (white, for example, is 255,255,255). If you find this interesting, here is a link to an interactive RGB chart. General Staff uses a similar system except instead of the RGB system each cell contains a value that represents various terrain types (road, forest, swamp, etc.) and another, identical, two-dimensional array, contains values that represent the elevation in meters. To make matters just a little bit more confusing, computer arrays are actually not two-dimensional (or three-dimensional or n-dimensional) but rather a contiguous block of memory addresses. So, the terrain and elevation arrays in General Staff which appear to be two-dimensional arrays of 1155 x 805 cells are actually just 929,775 bytes long hunks of contiguous memory. To put things in perspective, just those two arrays consume more RAM than was available for everything in the original computer systems (Apple //e, Apple IIGS, Atari ST, MS DOS, Macintosh and Amiga) that I originally wrote UMS for.

So, not surprisingly, a computer stores its map of the world in which it operates as a series of numbers ⁶⁾Yes, at the lowest level the numbers are just 1s and 0s but we’ll cover that before the midterm exams. that represent terrain and elevation. But, how does a human commander read a map? I posed this question to Ben Davis, a neuroscientist and wargamer, and he suggested looking at a couple of studies. In one article⁷⁾https://www.citylab.com/design/2014/11/how-to-make-a-better-map-according-to-science/382898/, Amy Lobben, head of the Department of Geography at the University of Oregon, said, “…some people process spatial information egocentrically, meaning they understand their environment as it relates to them from a given perspective. Others navigate more allocentrically, meaning they look at how other objects in the environment relate to each other, regardless of their perspective. These preferences are linked to different regions of the brain.” Another⁸⁾https://www.researchgate.net/publication/251187268_USING_fMRI_IN_CARTOGRAPHIC_RESEARCH reports the results of fMRI scans while, “subjects perform[ed] navigational map tasks on a computer and again while they were being scanned in a magnetic resonance imaging machine.” to identify specific, “involvement or non-involvement of the brain area.. doing the task.”

So, how computers and human commanders read and process maps is quite different. But, at the end of the day, computers are just manipulating numbers following a series of algorithms. I have written extensively about the algorithms that I have developed including:

“Algorithms for Generating Attribute Values for the Classification of Tactical Situations.”
“Implementing the Five Canonical Offensive Maneuvers in a CGF Environment.”
“Good Decisions Under Fire: Human-Level Strategic and Tactical Artificial Intelligence in Real-World Three-Dimensional Environments.”
“Current Methods to Create Human-Level Artificial Intelligence in Computer Simulations and Wargames”
Human Level Artificial Intelligence for Computer Simulations and Wargames.
An Analysis of Dimdal’s (ex-Jonsson’s) ‘An Optimal Pathfinder for Vehicles in Real-World Terrain Maps’

These papers, and others, can be freely downloaded from my web site here.

As always, please feel free to contact me directly if you have any questions or comments.

References[+]

References
↑1	When describing various AI processes I often use words like ‘see,’ ‘understand,’ and ‘know’ but this should not be taken literally. The last thing I want to do is to get in to a philosophic discussion on computers being sentient.
↑2	https://en.wikipedia.org/wiki/List_of_self-driving_car_fatalities
↑3	https://www.theguardian.com/technology/2016/jun/30/tesla-autopilot-death-self-driving-car-elon-musk
↑4	TIGER: An Unsupervised Machine Learning Tactical Inference Generator http://www.riverviewai.com/download/SidranThesis.html
↑5	Except in France where it’s RVB for Rouge, Vert, Bleu
↑6	Yes, at the lowest level the numbers are just 1s and 0s but we’ll cover that before the midterm exams.
↑7	https://www.citylab.com/design/2014/11/how-to-make-a-better-map-according-to-science/382898/
↑8	https://www.researchgate.net/publication/251187268_USING_fMRI_IN_CARTOGRAPHIC_RESEARCH

A Wargame 55 Years in the Making (Part 2)

9 Replies

After The War College I created a couple of non-wargames including Online Mysteries, a massive multiplayer online mystery game that was written for AOL’s WorldPlay. WorldPlay was envisioned to be a 3D online world populated with avatars. It was similar in concept to Second Life but, like a lot of great ideas, was ahead of its time. AOL shut WorldPlay down before most of the games, including Online Mysteries, launched.

Mysteries Unlimited screen shot (Windows) was a massively multiplayer online mystery game created for AOL/WorldPlay (click to enlarge).

By 2000 the game publishing industry was going through another convulsion of consolidations, buyouts and contractions. Publishers were producing fewer games but the ones that were being created had large teams, long development cycles and massive budgets. The days when an independent developer could pitch a game idea, get an advance and then develop it outside of a publisher’s studio were gone. And the last thing that the big publishers were interested in were wargames.

Over the previous fifteen years I had received inquiries from active duty military and Pentagon project managers about my wargames (known as Commercial Off The Shelf, or COTS, in Pentagon-lingo) and if I would be available to consult on various wargaming projects. Unfortunately, I was lacking a key prerequisite for this: a doctorate. I returned to academia, first to a small local college where I also taught computer game design and in 2003 I was accepted in the computer science PhD program at the University of Iowa (one of the oldest computer science departments in the world).

Before I ever set foot in MacLean Hall (the home of the Department of Computer Science at the University of Iowa) I knew what I would spend the next six years of my life researching and studying: tactical and strategic AI (I would eventually coin the phrase ‘computational military reasoning’ to describe this field). What I soon discovered was that very little work had ever been done in this research area. What was even more surprising was my discovery that most ‘professional’ military wargames (i.e. wargames used by the US Army, NATO, England, Australia, France, etc.) had absolutely no AI whatsoever. Instead, they employed ‘pucksters’ (usually retired military officers) who made all the moves for OPFOR (Opposition Forces, AKA ‘the enemy’) from another computer in another room.

Pucksters, or humans (usually retired military officers) who make the decisions and moves for enemy (or OPFOR) units during a wargame.

Pucksters are humans (usually retired military officers) who make the decisions and moves for enemy (Opposition Forces = OPFOR) units during a wargame. Note the sign OPFOR & EXCON (Exercise Control) over the puckster’s work station.

To earn a doctorate at an American ‘Research One’ university requires 90 graduate credits (about 30 classes), a GPA > 3.5 (out of 4.0) and passing three major examinations. The first examination on the road to a doctorate is the Qualifying Examination (or Q Exam as everyone calls it). The topic of my Q exam was “An Analysis of Dimdal’s (ex-Jonsson’s) ‘An Optimal Pathfinder for Vehicles in Real-World Terrain Maps’.” This is the area of computer science and graph theory known as ‘least weighted path algorithms’. GPS devices and Map apps use a least weighted path algorithm, except they’re only interested in roads; they don’t consider terrain, slope and other things (that are important to a military unit maneuvering on a battlefield).

Now, if you were to wander into the ivied halls of academic computer science (like MacLean Hall) and inquire of a tenured faculty member how to calculate the fastest path between two points on a sparse grid they would almost certainly reply to you, “Dijkstra’s algorithm.” Dr. Dijkstra invented his algorithm in 1956 and it works like this: first calculate the distance between every point on the map and every other point on the map. Then figure out the fastest path. Yeah, it’s that obvious, and painfully slow. In fact, it’s so slow that it isn’t used for GPS or game AI. In computer science we us ‘Big O’ notation to describe how fast (or slow) an algorithm takes to run. Dijkstra’s algorithm runs in O(|V|²). This means that as the number of vertices, or points on the map, (that’s the |V| part) increases, the time it takes for the entire algorithm to complete goes up by the square of the number of vertices. In other words, as the map gets bigger the algorithm gets a lot slower.

Dimdal, and I and most of the gaming world do not use Dijkstra’s algorithm, Instead we use A* (pronounced ‘A Star’) which was designed in 1968 primarily by Nils Nilsson with later improvements by Peter Hart and Bertram Raphael. Below is an example of A* used in General Staff (note that the algorithm doesn’t look at every point on the map, just ones that it thinks are relevant to the problem at hand). A* runs in O(n) time.

A screen shot of A* algorithm running. The green areas are where the algorithm searched for a least weighted path, the brown line is the shortest path (mostly following a road).

Graph showing the difference between Dijkstra’s algorithm and the A* algorithm. The blue line that increases rapidly shows that Dijkstra’s algorithm takes much more time as the map gets bigger. A* (the green line) is not affected as much by the size of the map.

As part of my research into computational military reasoning I made further modifications to A* to take into effect the slope of the terrain (which can affect speed of some units), the range of enemy units (OPFOR ROI, e.g. areas controlled by enemy artillery) and to avoid enemy line of sight (LOS). My MATE (Machine Analysis of Tactical Environments) project used all of these options:

A slide from my presentation to DARPA showing how my modified A* avoids enemy range of weapons. The likelihood of taking casualties is indicated by the darkness of the red coloring.

While working on General Staff I came up with a new optimization of the A* algorithm which I’ve called EZRoadStar. EZRoadStar first looks at the roadnet and attempts to utilize it for rapid troop movement. Only after ascertaining how far using roads will get it to its goal does the algorithm look for nonroad paths. EZRoadStar is much faster than traditional A*; especially for wargames and military simulations.

An example of the EZRoadStar least weighted path algorithm. What's the fastest way point A to point B (the yellow line)? Taking the road, of course. This algorithm looks at a battlefield like a commander and utilizes the roadnet first before looking at other options. Click to enlarge.

An example of the EZRoadStar least weighted path algorithm. What’s the fastest way from point A to point B (the yellow arrow)? Taking the road, of course. This algorithm looks at a battlefield like a commander and utilizes the roadnet first before looking at other options. Click to enlarge.

Well, this wargame may be 55 years in the making and it looks like describing some of the key things that went into it may take almost as long. Clearly, I’m going to have to continue this story with yet another post. We’ve just barely scratched the surface of my work on wargame AI. The next installment will (hopefully) cover algorithms for ‘the five canonical offensive maneuvers’ (i.e. The Envelopment Maneuver, The Turning Maneuver, Penetration, Infiltration and Frontal Assault. These are the algorithms that are ‘under the hood’ of General Staff. If any of my readers would like to know more about these topics (links to my published papers on the subject or whatever) please drop me a line at Ezra [at] RiverviewAI.com.

New, Faster Pathfinding AI