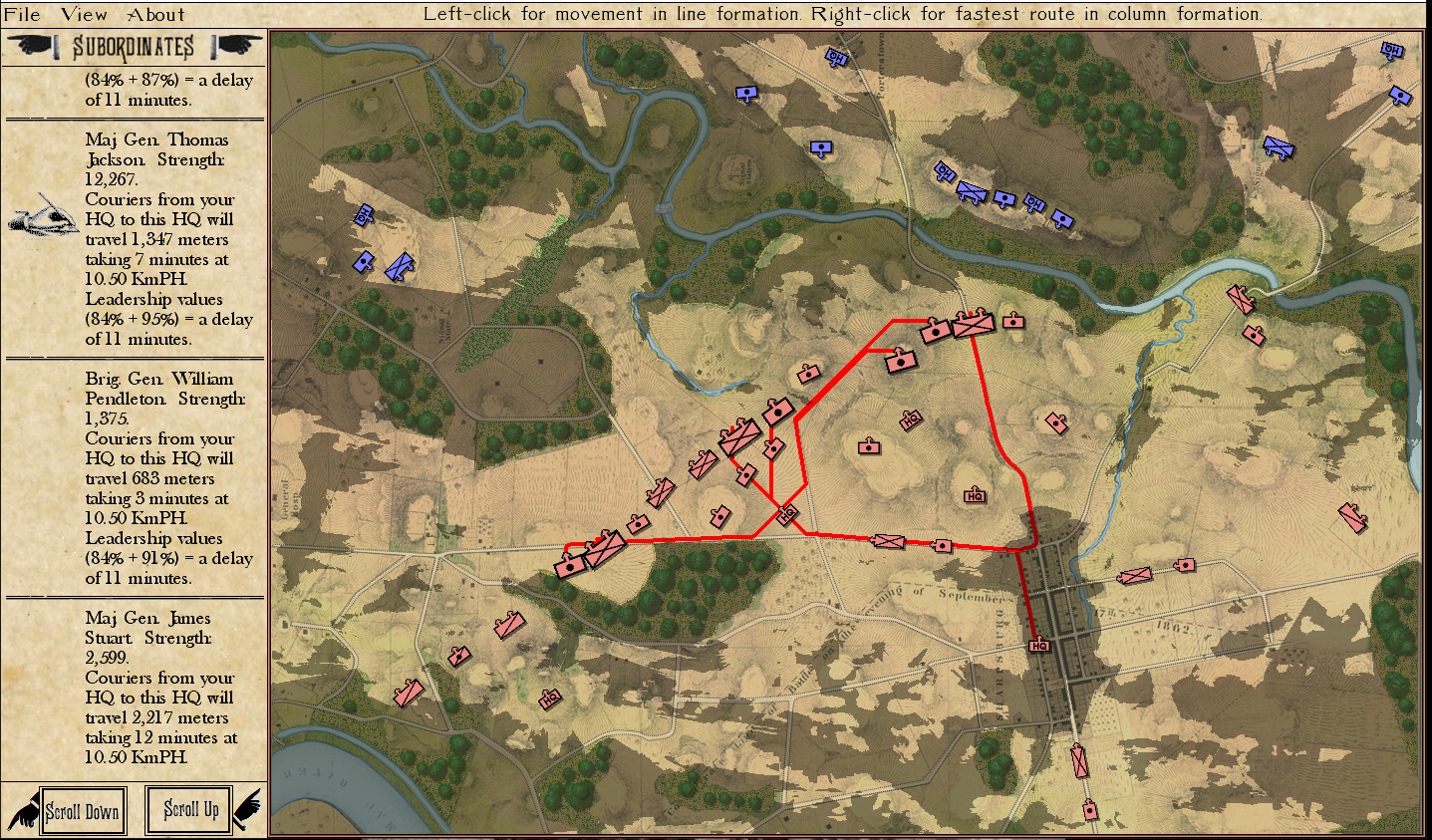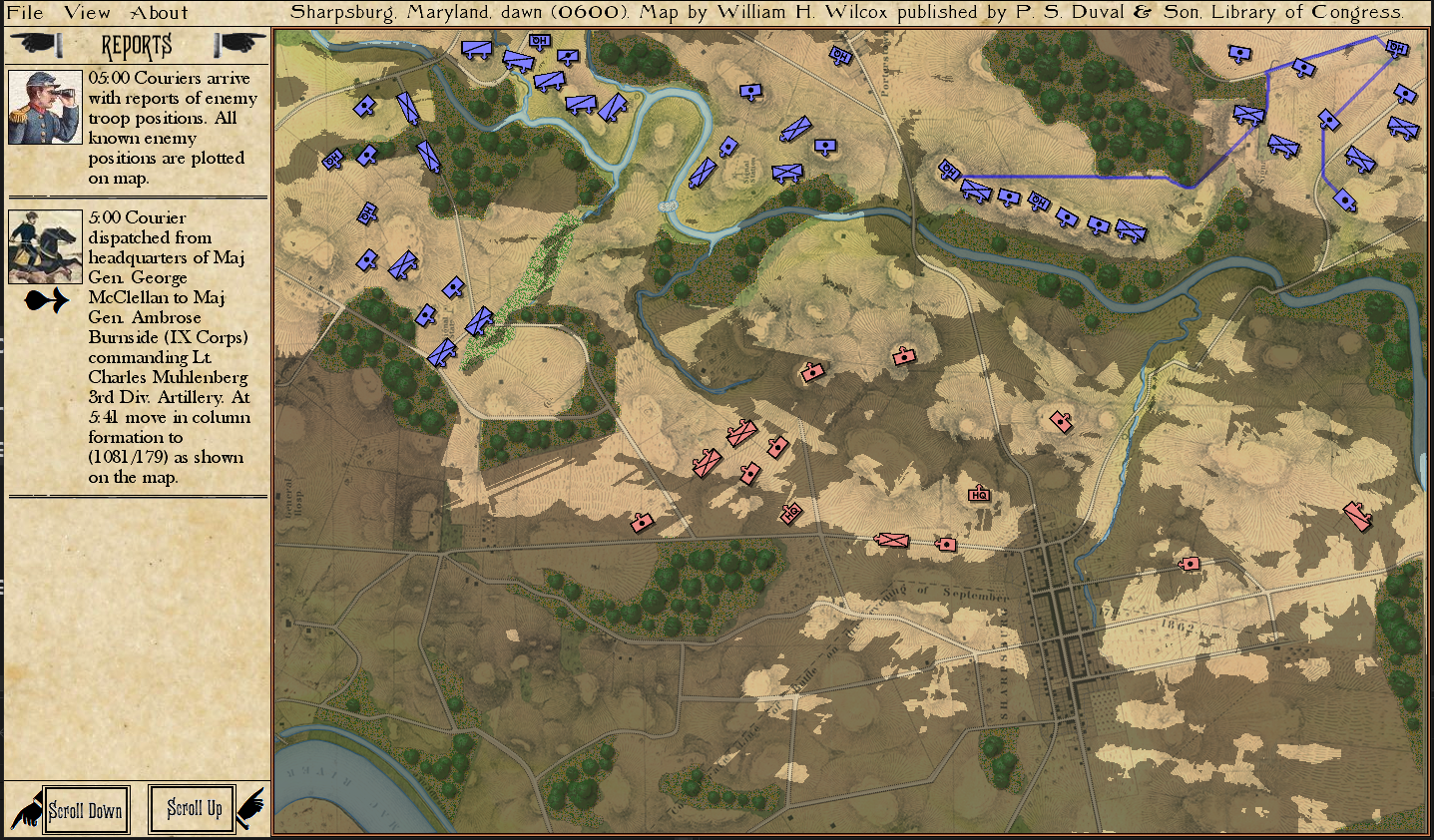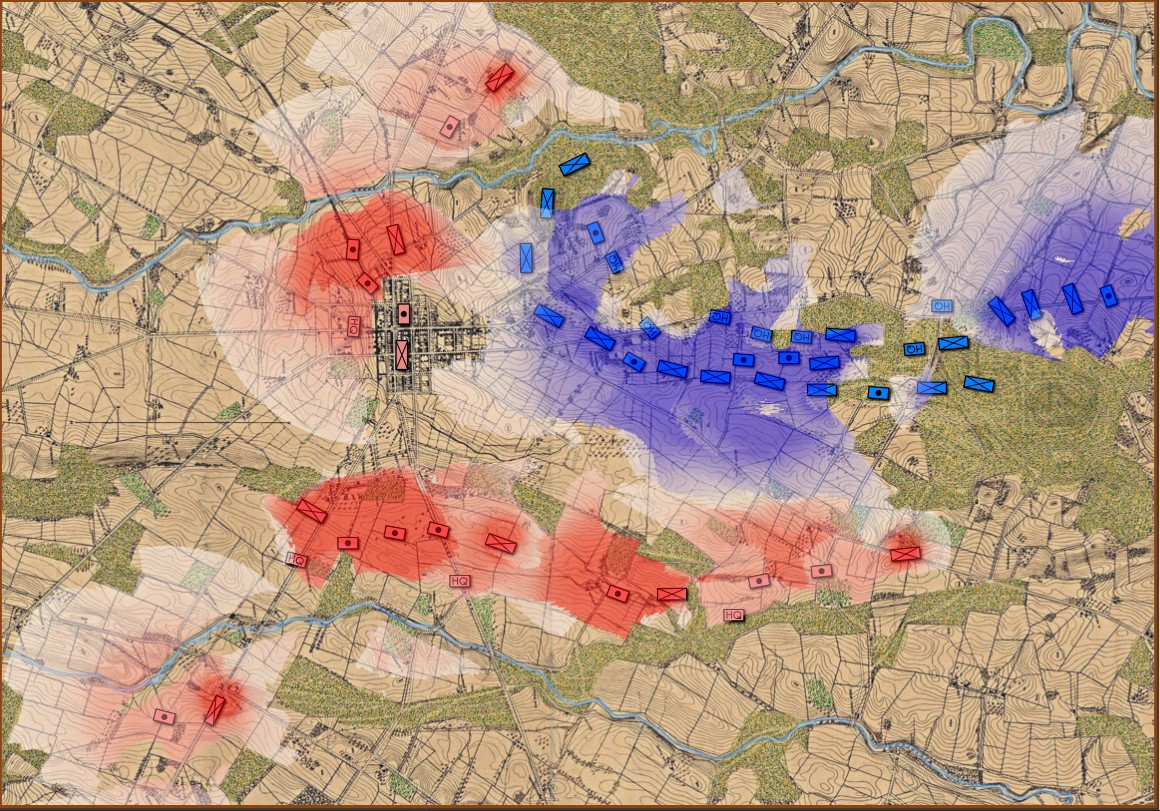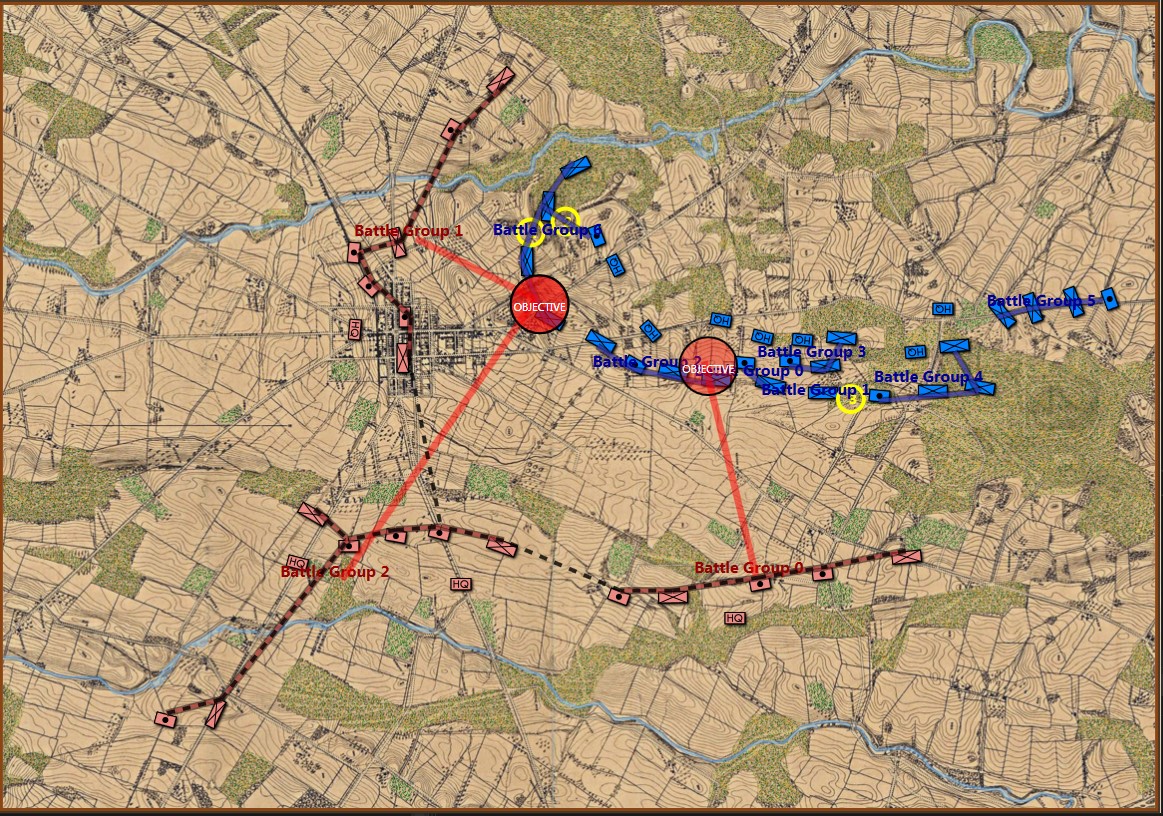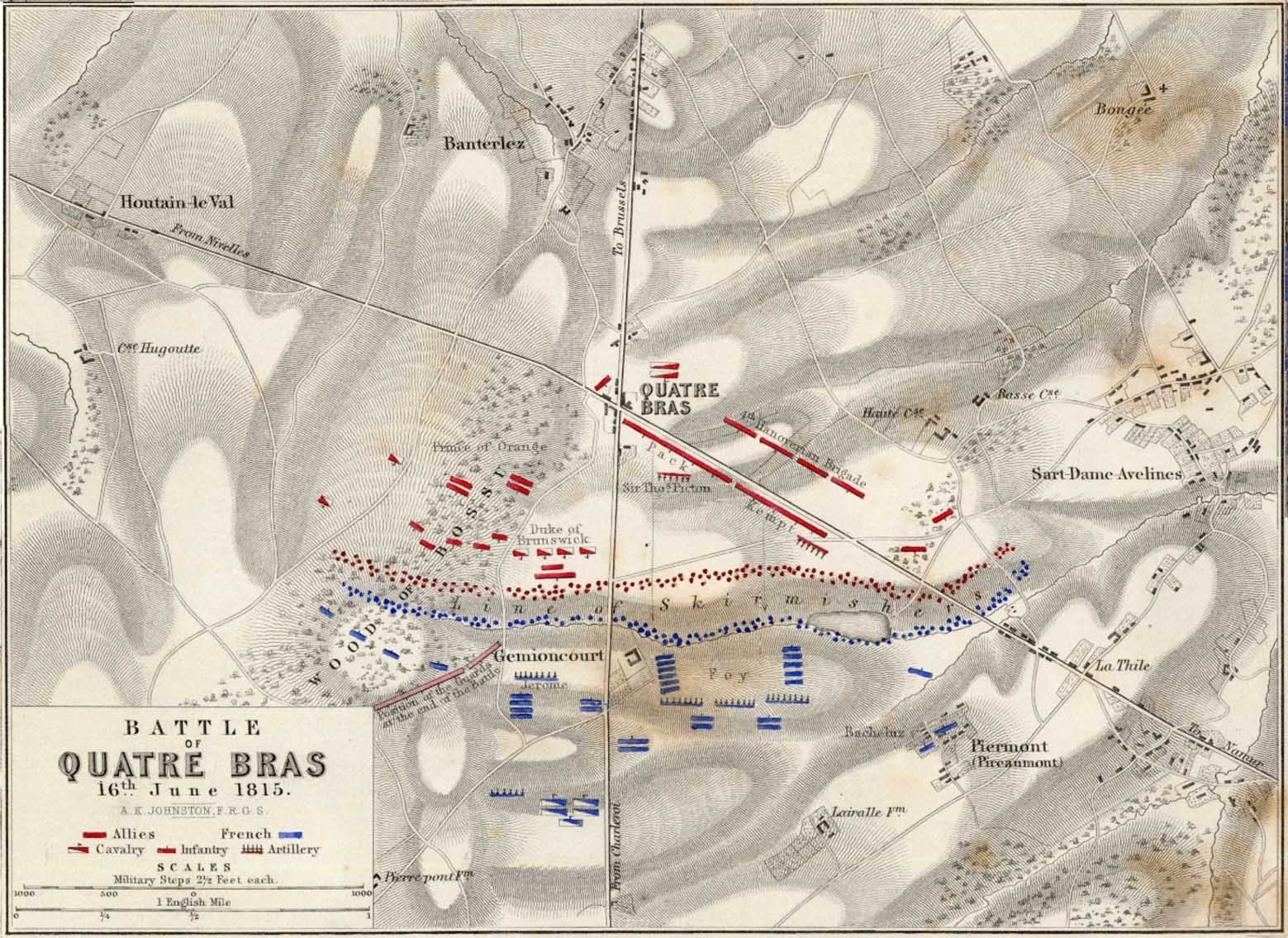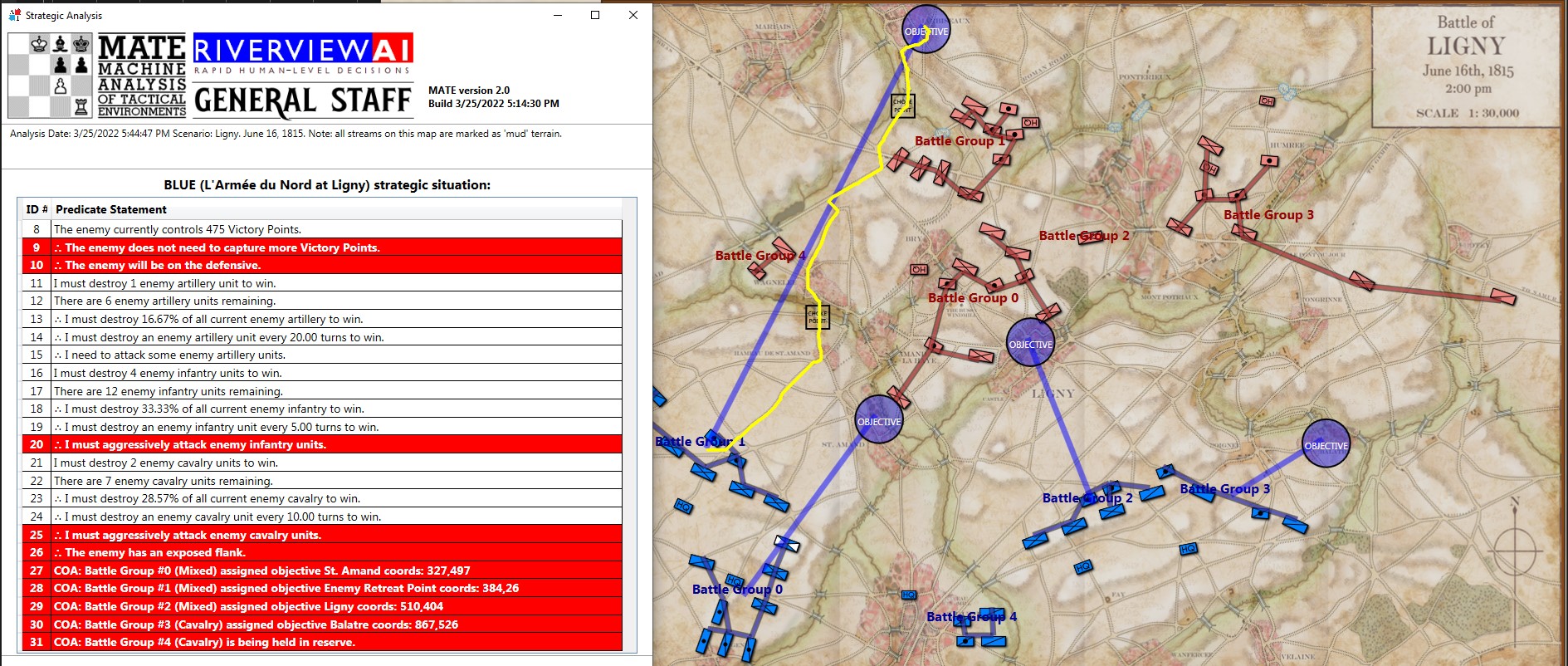
This screen shot is an example of the design flaw that has now been corrected. Units don’t instantly change from line to column formation. Note that the red infantry unit is first in line formation (facing northwest), it receives orders from the HQ to switch to column formation advance to a position, switch to line formation, travel in line formation, then switch to column formation and travel in that formation. If you observe closely, the unit one instant is in column formation and the next it is in line formation occupying a different portion of the terrain.
The first lecture I would give at the beginning of every semester started: “The greatest asset you can have as a programmer – or as a human being – is the ability to admit that ‘I screwed1)Full disclosure: I wouldn’t say ‘screwed up’. If you want to get an undergraduate’s attention use the ‘f word’. up’ fifty times a day if necessary. Because, until you admit you made a mistake, you can’t find you mistake. And until you find you mistake you can’t fix your mistake. The first step to fixing a mistake is to first admit you made it.”
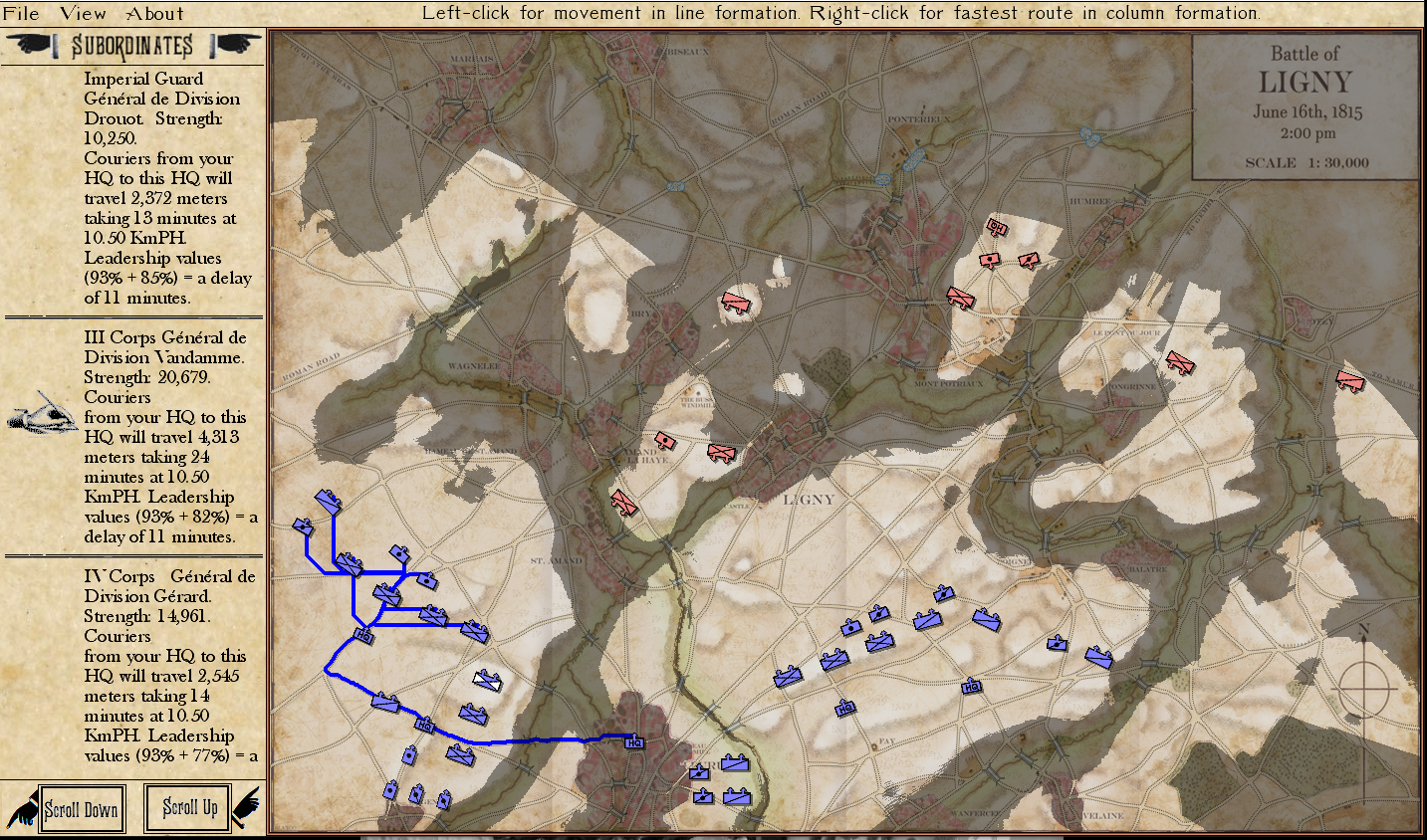
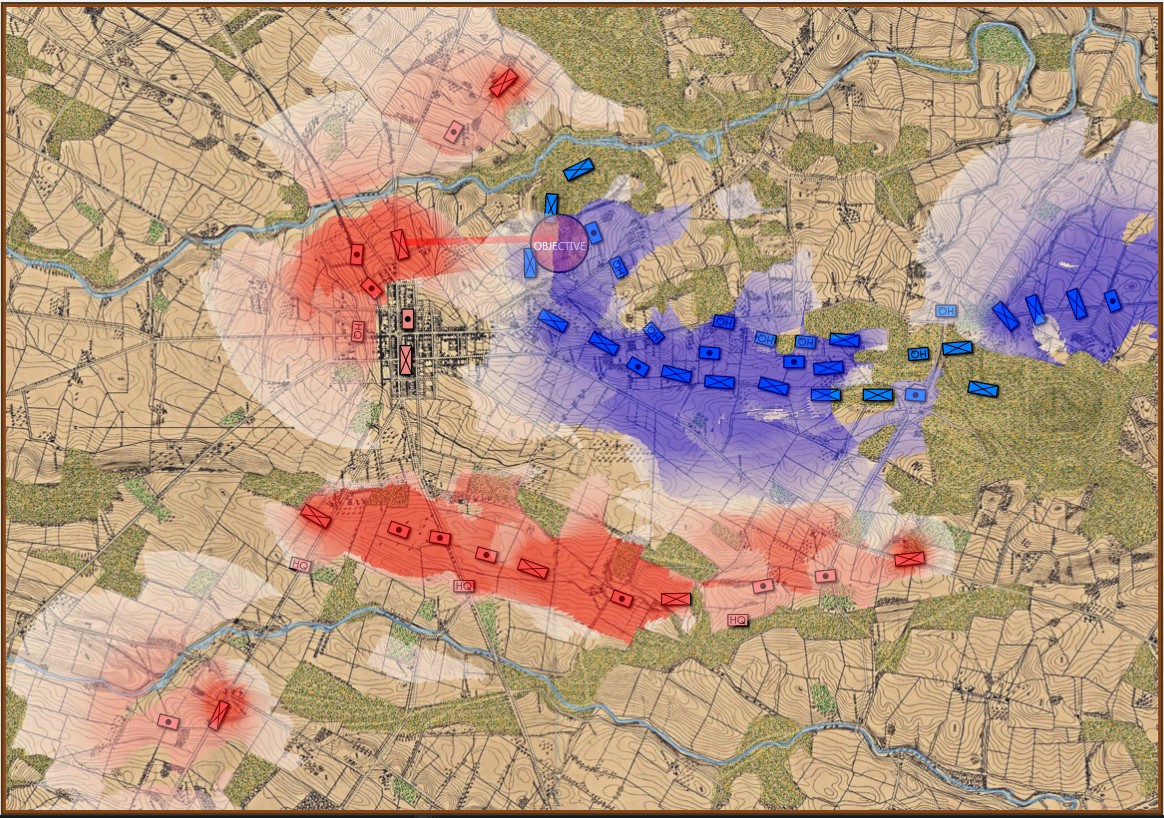
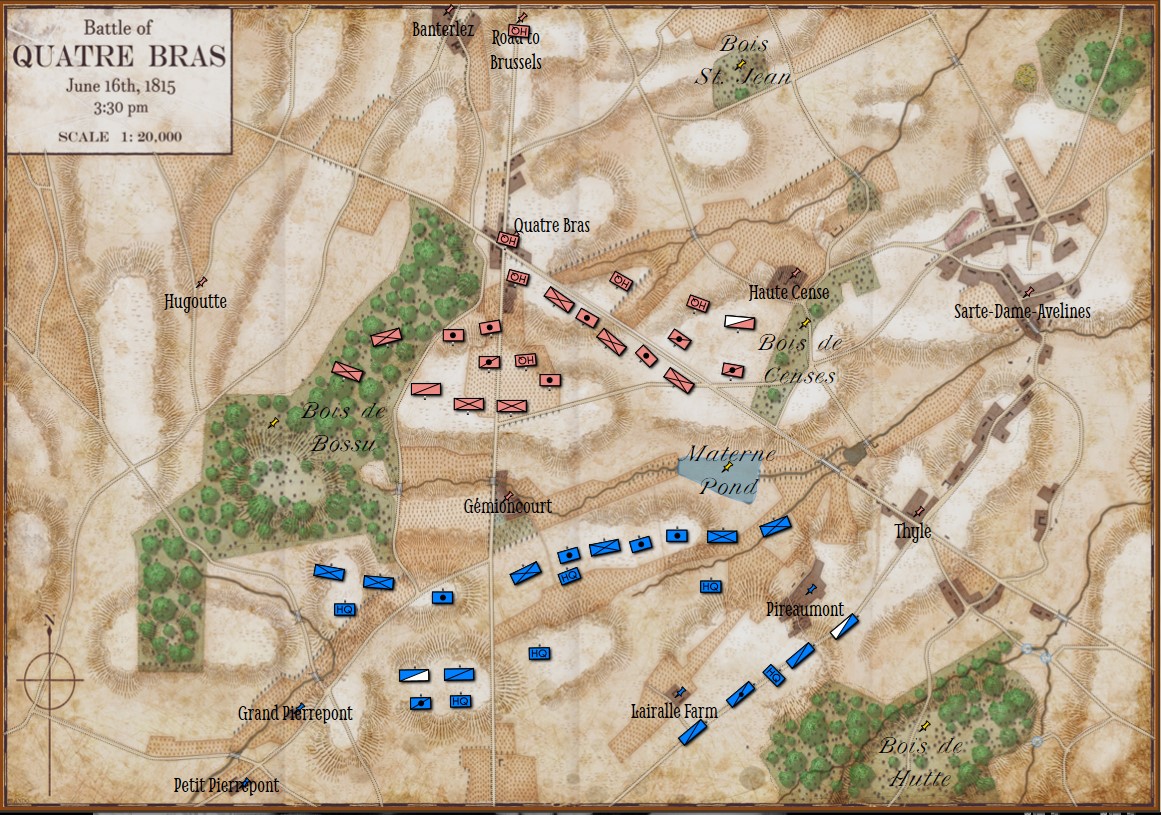
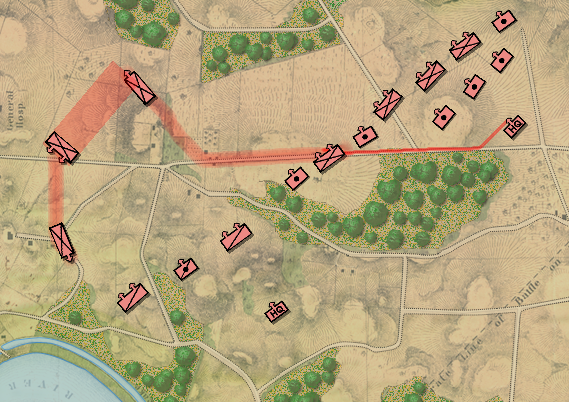
In the above screen shot there is a glaring error and I didn’t see it for years. In my defense, nobody else saw it, either. The screen shot, below, shows the correct movement and unit formations:
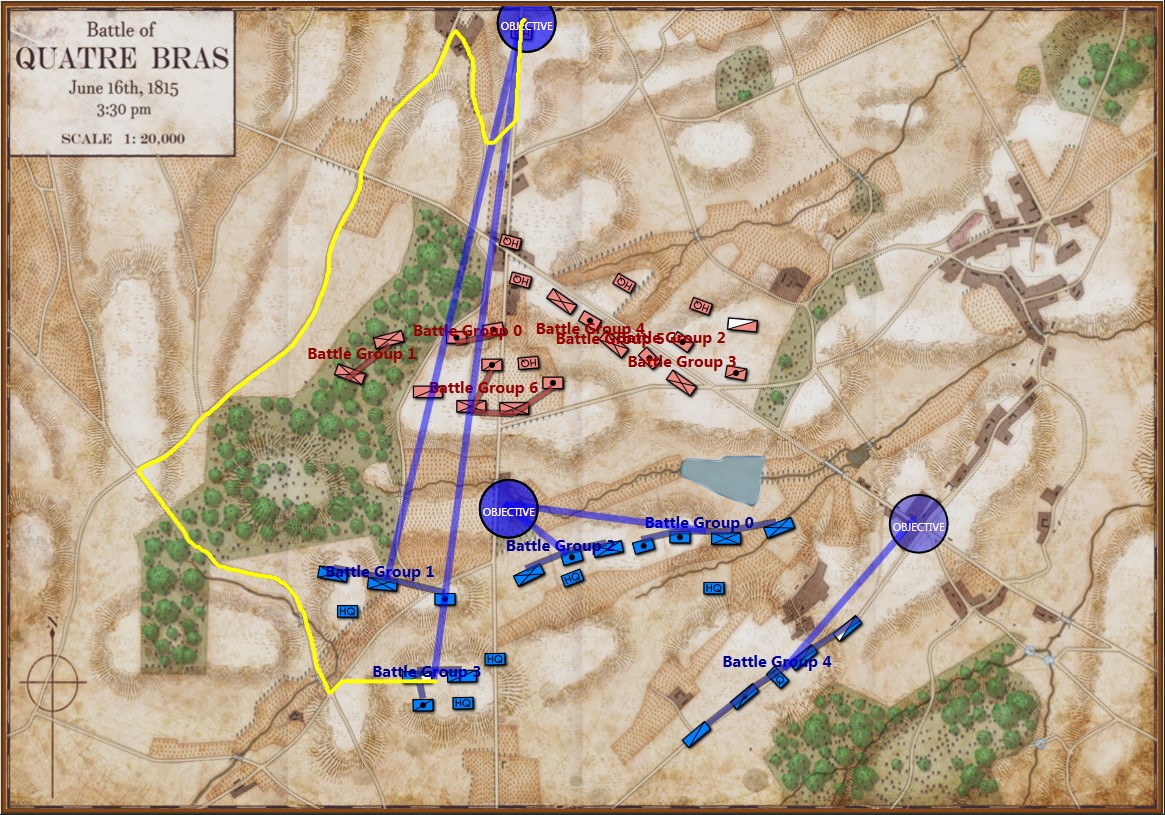
In this screen shot you can see that the unit is switching formations correctly. Note how the unit first changes from line to column formation by ‘a left face’ command, then moves in column formation, avoiding the artillery battery, moving on to the road and advancing to the assigned location where the unit stops, changes into line formation via another ‘left face’, advances in line formation as ordered until it reaches its destination, stops, forms column by another ‘left face’ and then advances to its destination.
Without getting into details, this was a pretty complicated fix. Looking for help with this, and some MonoGame2)MonoGame is a community supported version of Microsoft’s XNA which was created specifically for making cross-platform games. Microsoft stopped all support for XNA in April 2014. Previously, I had used XNA for some work that I had done for the US Army and the Department of Defense and thought it had great potential for creating computer wargames and simulations. specific problems, I encountered Matthew T. from the MonoGame forum who very kindly volunteered to help. Not only did Matthew fix the line / column formation problems but he identified and fixed a bug with the typography for the game, too:

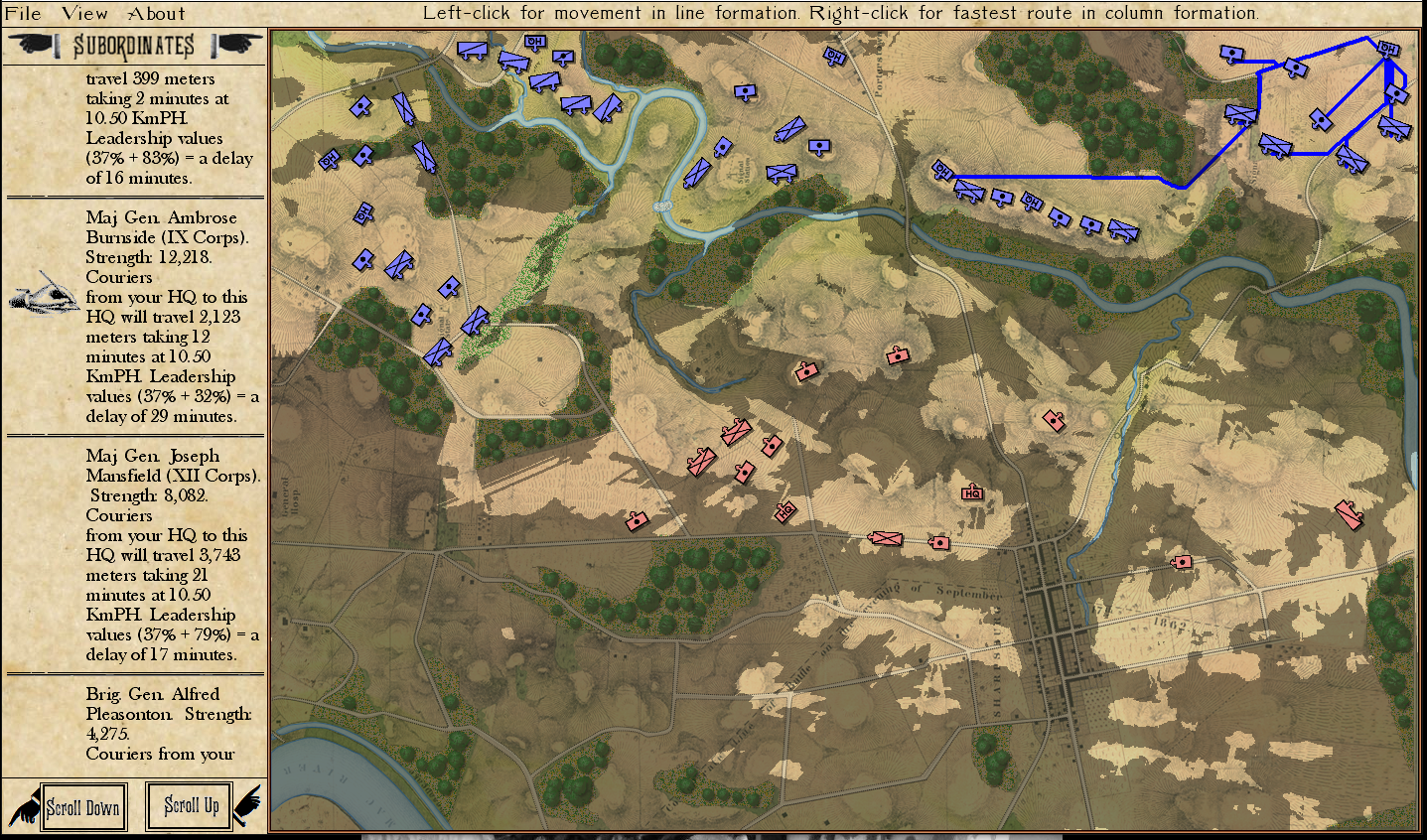
These two screen shots show the difference in the clarity and spacing (called kerning) of the letters. In the left screen shot notice the lowercase ‘g’ in Debug and the spacing of the letters in the word ‘positions’. In the right screen capture, after applying Matthew’s typographical fixes, the letters are clear and properly spaced.
Matthew is also cleaning up the codebase. I have a tendency to write code ‘fast and furious’ and then hope to go back and optimize and clean it up later. Matthew has already begun cleaning it up and has reduced the codebase by something like 7,000 lines of code! Furthermore, Matthew has also sped up the load time and the time between game turns from about a minute to about 10 seconds (obviously, time varies based on scenario).
Steam Update
Darin Jones has been working on the Steam side. He created the Installer and is working on setting up Player versus Player (PvP) leveraging Steam’s built-in features. While this has been a steep learning curve, Darin has made some significant progress:
Screen shot of Steam Player vs. Player invitation for General Staff: Black Powder. This is not a Play by Email (PBEM) system, rather it uses Steam’s internal messaging system
Darin is also setting up a ‘Workshop’ area where you can upload scenarios, armies and maps that you create and want to use in a PvP game.
What’s Next
Our goal remains to get General Staff: Black Powder into beta-testing (that’s you guys playing with it) as soon as possible. We want to use the Steam PvP method, above, as the vehicle for testing. I’m grateful for the emails that I’ve received that are encouraging me to not rush General Staff: Black Powder out before it’s ready and to deliver a solid game (see also, Gabe Newall on why game delays are OK: ‘Late is just for a little while. Suck is forever.’).
As always, please feel free to contact me directly at Ezra[at]RiverviewAI.com.
References
| ↑1 | Full disclosure: I wouldn’t say ‘screwed up’. If you want to get an undergraduate’s attention use the ‘f word’. |
|---|---|
| ↑2 | MonoGame is a community supported version of Microsoft’s XNA which was created specifically for making cross-platform games. Microsoft stopped all support for XNA in April 2014. Previously, I had used XNA for some work that I had done for the US Army and the Department of Defense and thought it had great potential for creating computer wargames and simulations. |